Cornell Virtual Workshop > Parallel Programming Concepts and High Performance Computing > Data Communication

Data Dependency

Data dependency occurs when a computation depends on the results of a previous computation. When data dependency is present in an algorithm or computation, the program must execute the operations in the intended order to arrive at the correct result. Any reasonably complex algorithm will involve some degree of data dependency.

In serial programming, the program will execute statements sequentially and in the same order they appear in the code. Thus, managing data dependency in a serial program is a matter of writing the code statements in the correct order. In parallel programming, where some portions of the code are executed simultaneously, managing data dependency is more complicated.

Recognizing which parts of your code involve data dependency is the first step to ensure correct parallel computation. The first two examples below show simple computations with no data dependency. These are followed by two examples with significant data dependency, showing how the algorithm you choose may reduce the data dependency in your program.

Example 1: No dependency

Consider a program that takes an input array and applies a unary function to each element to compute an output array. In this case, each element of the result can be computed independently, so the program is highly amenable to parallelization.

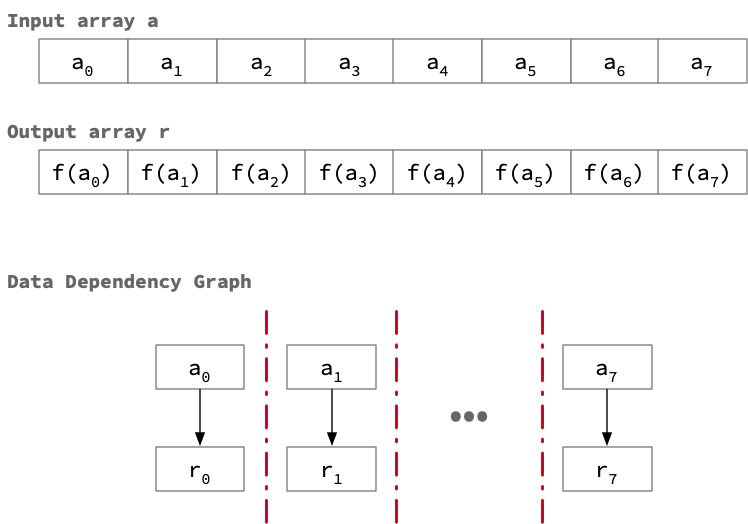
A program accepts an input array and applies a function to each array element to produce an output array. Since the data required to compute a particular output array element depends only on the corresponding input element, each element could be computed by a different task. — A program accepts an input array and applies a function to each element to produce an output array. Each output element is independent of the other outputs. Since the data required to compute a particular output array element depends only on the corresponding element from the input array, each output element could be computed by a different task.

Example 2: No dependency

Suppose a program accepts two input arrays, A and B, and computes an output array by combining corresponding elements of A and B. In this case, the program is still easy to parallelize because the inputs and outputs are all independent from each other; that is, no operation depends on the outcome of a previous operation.

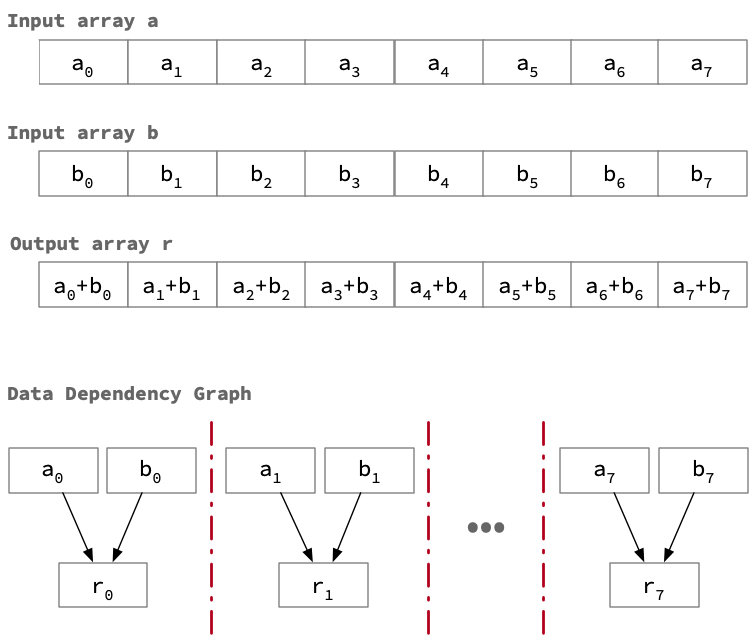
A program accepts two input arrays and computes the pairwise sum to produce an output array. Since the data required to compute a particular output array element depends only on the corresponding elements from the input arrays, each output element could be computed by a different task.

Example 3: High dependency

The choice of algorithm impacts data dependency. Consider a program that computes the sum of an input array. In one implementation, the program starts with the first element and accumulates the sum element-by-element to arrive at a final result. This algorithm produces a pattern of data dependency that is resistant to parallelization.

A program accepts an array and computes a scalar sum of the array elements. In this implementation, each computation depends on the result obtained for the prior computation, so the computation cannot be usefully parallelized. — A program accepts an array and computes a scalar sum of the array elements. In this implementation, each computation depends on the result obtained for the prior computation, so the algorithm cannot be usefully parallelized.

Example 4: Reduced dependency

An alternative algorithm to compute an array sum might add consecutive pairs of elements to produce a new array that is about half the original input size, then repeat the process of combining pairs of elements until the output array reduces to a single element. In contrast to the first array summation algorithm, this alternative algorithm can take advantage of parallel tasks — at each stage of the reduction, each pairwise summation can be performed by a separate task. You can see this in the dependency graph below: it has the same number of pairwise summations as the first graph, but the pairs are rearranged so that more of the sums can be done in parallel.

A program accepts an array and computes a scalar sum of the array elements. In this implementation, the algorithm produces an intermediate result by adding consecutive elements of the input array. This process is repeated until the result array has only one element. — A program accepts an array and computes a scalar sum of the array elements. In this implementation, the algorithm produces an intermediate result by adding consecutive elements of the input array. This process repeats until the result array has only one element. In this example, four parallel workers compute the first intermediate array, two parallel workers produce the second intermediate array, and one worker executes the final add operation. Because much of the work can be done in parallel, it only takes three stages to compute the result, compared to the seven stages required to compute the array sum using the first algorithm.

Back