Cornell Virtual Workshop > Parallel Programming Concepts and High Performance Computing > Thinking Big

Parallelization Strategy

A rudimentary parallelization strategy is to split each iteration of an outer loop into separate computations and distribute these computations among parallel tasks. Although the outermost parallelizable loop in the program is one of the most important sites for scrutiny, simply spreading it across tasks may not be the best design strategy for scalable parallel programs due to data dependency and messaging overhead.

Domain decomposition and communication

Dividing data and computations over tasks is domain decomposition; this is a type of data parallelization, as discussed earlier in this topic. If we think of the data arranged in N-dimensional space (N=2 in the illustration), the outermost loop might be traverse one of these dimensions. In that case, parallelizing on that loop involves slicing the domain into strips one (or a few) data elements wide.

(Left) A two dimensional 6 by 6 grid representing the data coordinates visited by a 2-deep nested for loop. Each grid point is connected to its four nearest neighbors to make a Von Neumann grid. The gridlines represent a possible data dependency for this example. (Right) If the loop is parallelized by splitting the outer loop over multiple tasks then each task operates on one strip of the grid. Here, each task is assigned to one column. — The figure represents the data points computed by a 2-deep nested for loop as a 2-dimensional grid. If the nested for-loops were parallelized by distributing the outer loop across tasks (represented here as grey bars), each task would operate on a strip of the data grid (a column in this case). Suppose the gridlines represent dependencies in the computation; a message will need to be sent and received between any two grey bars that are connected by one or more grid lines. Communication overhead will be reduced if all the data required to satisfy a set of dependencies on a connected task can be packed into a single message.

Suppose there are data dependencies between the adjacent strips so that each iteration requires sending data between tasks. In this case, the amount of data communicated is proportional to the circumference of each strip. One limitation of this parallelization scheme is that the only way to use more tasks is to increase the number of data columns. A second limitation is that increasing the number of data rows increases both the amount of computation and the amount of communication required per task. Communication between tasks represents parallel overhead, so increasing the amount of time individual tasks spend communicating impacts performance.

A more scalable parallelization strategy is to divide the data into compact domains, such as blocks, instead of strips, which minimizes the communication and keeps the amount of data that needs to be communicated after each iteration to remain roughly constant as the number of tasks increases. A program designed around compact domains can be adapted to additional data columns or rows by adding more tasks.

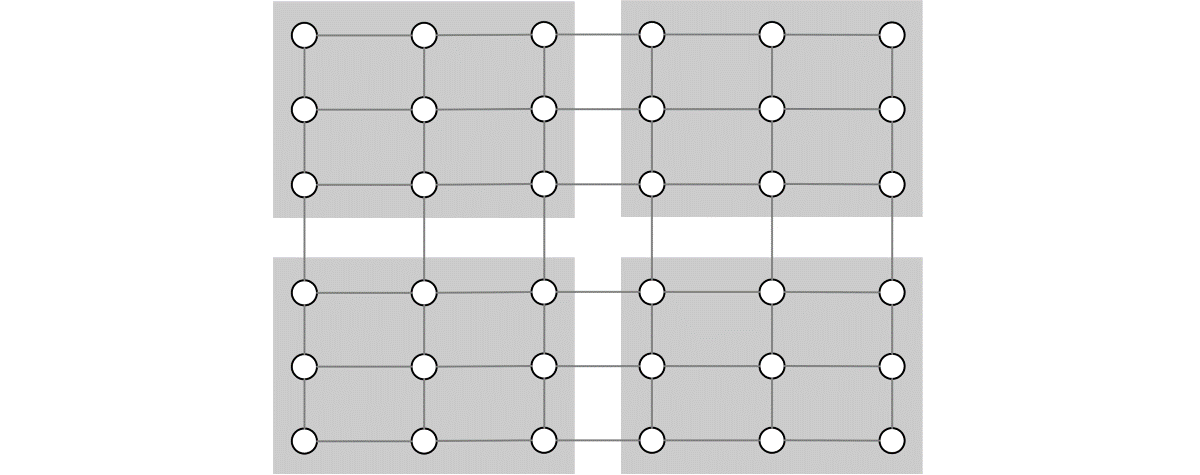
A two dimensional 6 by 6 grid representing the data coordinates visited by a 2-deep nested for loop. Instead of splitting the data so each taks is assigned to one column, the data is split into four 2 by 3 blocks and each block is assigned to a task. — The diagram represents the data points computed by a 2-deep nested for-loop as a 2-dimensional grid. If the nested for-loops were parallelized by distributing sections of the inner and outer loop across tasks, each task would operate on a compact domain (a block in this case). While each task has some messaging responsibility, the number of messages per task does not increase as the data size increases. Instead, new data can be partitioned into new blocks and assigned to additional tasks.

To leverage multicore processors, consider parallelizing some computation within tasks using shared memory parallelism. In the example above, this would allow computation on the grid points that are contained within the grey boxes above to be additionally parallelized without creating more connections to other grey boxes.

Foster's Design Methodology

Ian Foster's book Designing and Building Parallel Programs is a good resource for parallel design strategy and methodology. The book is available online at https://www.mcs.anl.gov/~itf/dbpp/. According to Foster's methodology, program design involves four steps: partitioning, communication, agglomeration, and mapping.

The first step is partitioning the computation and data into the smallest viable units. Foster recommends starting with the largest or most frequently accessed data first. This step is similar to the data and functional parallelism described in the program design section. Ideally, partitioning will result in a collection of primitive tasks.

The second step is to map out the communication patterns between primitive tasks. In our examples involving the nested for-loop, the computations depended on the nearest neighbors in the 2-dimensional grid, and this pattern of communication impacted the efficiency of different parallelization strategies.

The agglomeration stage considers the communication cost, task creation cost, and sequential dependence of the primitive tasks. For instance, group tasks with sequential dependence into a single unit; parallel workers cannot perform this work efficiently. Bundle primitive tasks to maximize communication within the bundle and minimize communication outside of the bundle. Combine bundles such that each parallel task performs a reasonable amount of computation relative to the cost of creating the task.

In the final stage, different groups of primitive tasks are mapped to specific hardware. The general strategy is to use multiple nodes to increase the amount of work done in parallel while keeping parallel workers that communicate frequently on the same node or processor. Optimal mapping might require a hybrid programming style that combines both shared and distributed memory styles.

Back