The 1D Wave Equation: Our Physics Model
Let's implement a differentiable physics simulation. We'll use the 1D acoustic wave equation:
\[ \frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2} \]
Where:
- \( u(x,t) \) is the wavefield (pressure/displacement)
- \( c(x) \) is the wave speed (what we want to estimate)
Finite difference discretization:
\[ u_{i}^{n+1} = 2u_{i}^{n} - u_{i}^{n-1} + \frac{c_i^2 \Delta t^2}{\Delta x^2}(u_{i+1}^{n} - 2u_{i}^{n} + u_{i-1}^{n}) \]
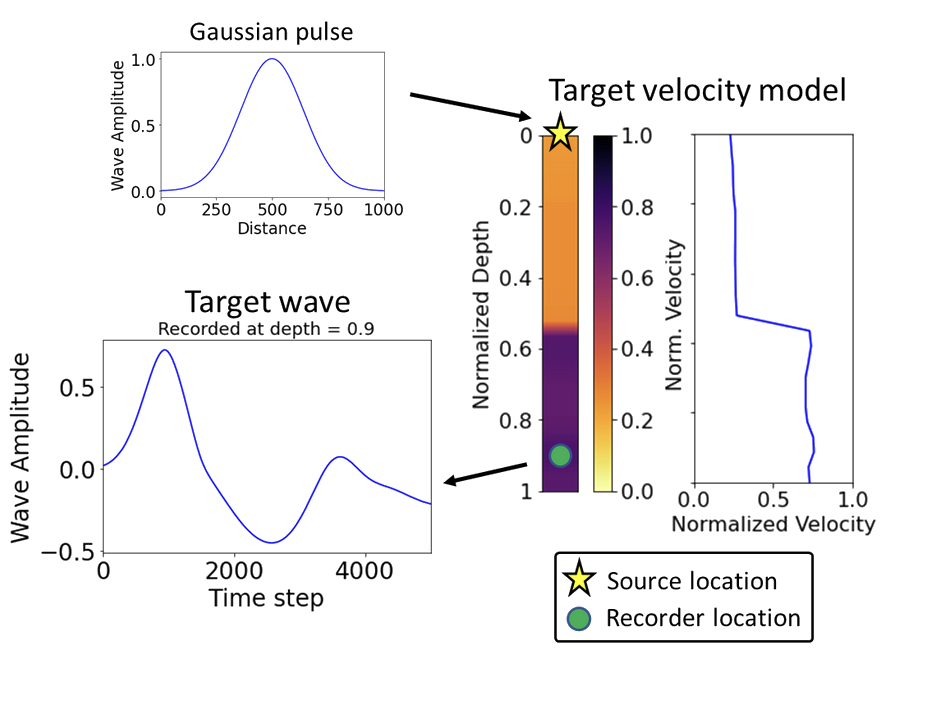
Initial conditions: Gaussian source
\[ u_0 = \exp\left(-5(x - 0.5)^2\right) \]
The Forward Problem: Simulation
The forward problem is to simulate the behavior of \( u(x,t) \) given an initial state and the wave speed profile \( c(x) \). We will solve this using a finite difference method. By rearranging the central difference approximation, we can find the wave's state at the next timestep based on its two previous states:
\[ u_i^{n+1} = c_i^2 \frac{\Delta t^2}{\Delta x^2} (u_{i+1}^n - 2u_i^n + u_{i-1}^n) + 2u_i^n - u_i^{n-1} \]
We can implement this time-stepping loop in JAX. Using @jit, this loop will be compiled for high performance.
©
|
Cornell University
|
Center for Advanced Computing
|
Copyright Statement
|
Access Statement
CVW material development is supported by NSF OAC awards 1854828, 2321040, 2323116 (UT Austin) and 2005506 (Indiana University)
CVW material development is supported by NSF OAC awards 1854828, 2321040, 2323116 (UT Austin) and 2005506 (Indiana University)