HPC's path to petaflop/s, and on to exaflop/s, has not followed a straight line. The evolution of high-end systems has pushed the boundaries of technology on several fronts at once. The big reason for this is that HPC has tended to rely more and more on parallel processing based on commodity parts, which means that all sorts of advances in per-component cost and power efficiency must be incorporated into the design of today's systems.

CPUs have of course shrunk to ever-smaller sizes, such that many of them now fit on a single chip while consuming about as much power as the chips of the past. This trend favors hierarchical designs consisting of large networks of multi-core processors, each of which is host to a little network of CPU cores. These little networks of cores can readily share memory, which leads to systems (and applications) that have aspects of both shared- and distributed-memory parallelism.

In the meantime, GPUs have proven that SIMD computation can be very power-efficient. CPUs have been increasing their SIMD capabilities accordingly. This provides yet another style of parallelism that must be considered in contemporary HPC systems: vector processing, which allows CPUs to perform floating point operations on many pairs of operands simultaneously. (Ironically, vectorization goes back decades as a performance-boosting technique; it is interesting to see it reassuming importance.) The SIMD capability of each core adds yet another layer to the bottom of the hierarchy.

The three levels in this hierarchy of components can be visualized as three dimensions in space. In HPC parlance, "scaling up" often means adding threads of computation within a node, while "scaling out" generally means adding nodes. Thus the height and width of our space would then be OpenMP threads (say) in the vertical dimension, and MPI processes in the horizontal one. But to complete the picture, we should include the depth provided by vector processing. It is therefore natural to refer to SIMD capability as "scaling deep". Envisioned in this way, we see that HPC takes advantage of the three distinct forms of parallelism that have been developed for commodity hardware.

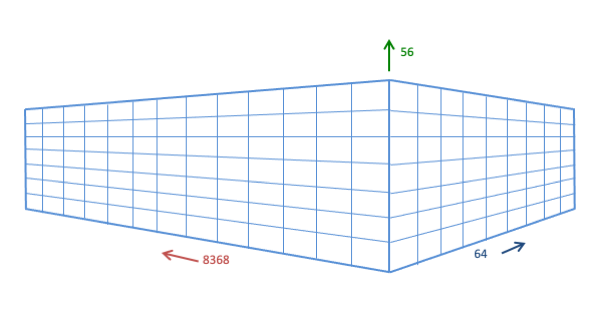
In advanced cluster architectures, such those leveraged by the (former) Stampede2 and Frontera clusters at TACC, how important are these dimensions relative to each other? We can construct a kind of computational volume for the SKX portion of Stampede2 or the CLX portion of Frontera if we multiply the maximum number of each type of parallel element that is available:

Computational volume = (nodes) x (cores per node) x (vector flops per cycle per core)

Stampede2/SKX:
Computational volume = 1736 x 48 x 64

Frontera/CLX:
Computational volume = 8368 x 56 x 64

The "nodes" number is really more of a conceptual upper bound. On a shared cluster, you may not always find that it is feasible to scale to 1000s of nodes with MPI, or that you will be granted access to all the nodes to run a single large job. (Furthermore, in Stampede3, the number of SKX nodes has been reduced to 1060.)

The "cores per node" number refers to physical cores rather than hardware threads. Hyperthreading was formerly enabled on the Stampede2 SKX nodes, which means that 2 hardware threads were activated per core, allowing 2 software threads to be processed concurrently on each core. Some applications might be able to make effective use of 48*2 = 96 (or more) software threads; however, the number in the "scaling up" dimension remains at 48, because hyperthreading simply enables more efficient use of existing resources and does not add any resources to the processors in a node. Hyperthreading is not currently enabled on the Stampede3 SKX nodes or the Frontera CLX nodes, since the potential benefit of using more threads is typically not as great for HPC codes.

The "vector depth" number assumes that on every cycle, both VPUs in a core will execute fused multiply-add (FMA) operations on full vectors of floats: 2 VPUs/core x 16 vector floats/VPU x 2 FLOPs / vector = 64. This number is roughly comparable to the number of cores available per node on each system, making vectorization appear to be comparable in importance to multithreading. However, such a complete degree of vectorization can be hard-to-impossible to achieve in practice.

The conclusion is that all three dimensions of scaling may be worthy of attention for numerically intensive, parallel codes that run on advanced, multi-core clusters. Therefore, we proceed to a set of three easy exercises to introduce you to each dimension in turn.