As mentioned, for large and small arrays, you should always try to arrange your data so that the elements are accessed with unit (1) stride. An easy illustration should be enough to convince you that the penalty for not doing so can be pretty severe.

Compiling the above Fortran code with all optimization and vectorization disabled (-O0), then running it for various strides (the istride variable above) should result in a curve like the red one in the figure below. Click here for the full C code that was actually used to produce the data in the figure.

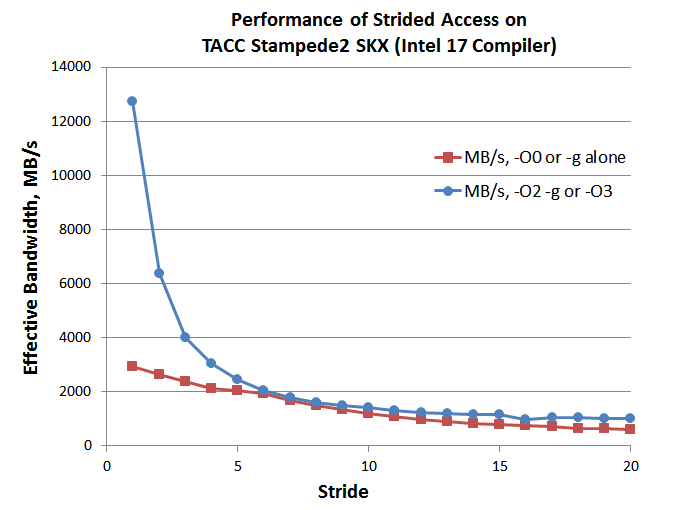
For the red curve, optimization is turned off in order to highlight the main effect: the lengthening of the access time as more and more cache lines must be fetched from main memory. For the blue curve, compiler optimizations such as vectorization are introduced, and the benefit of stride-1 becomes more pronounced. Even just the default level (-O2) builds in SIMD instructions that particularly boost small-stride performance, because multiple arguments (vectors) can be loaded, computed, and stored every cycle. (We will return to the subject of how to choose the right compiler options in a later section.)

Arrays having two or more dimensions show us another aspect of the stride question. Let's look at a matrix, an array of rank 2. It turns out that different languages have different orders for memory layout in matrices (or more generally, in multi-dimensional arrays). Fortran uses column-major order, that is, the elements of a matrix are contiguous in memory as you go down the columns. This means that in order to achieve stride 1, you'll want to iterate over the first index of the matrix in your innermost loops, i.e., iterate over rows preferentially. C is the opposite; it is row-major, so you will want to iterate over the columns (last index) when you have the choice.

The further implication is that if you arrange your loops in the wrong order, you will effectively be striding through your array with a step size equal to the entire length of the columns (Fortran) or rows (C). Sometimes the compiler will be able to detect such a poor choice and reorder the loops on your behalf—but why take that chance?