Maximizing the Use of Shared Memory

Shared memory can improve GPU utilization by providing faster access speeds to data, especially any data that is needed by more than one thread. In our final GPU performance topic, we will cover the process of tiling, a technique that prioritizes the efficient use of shared memory. A similar technique is often employed to maximize cache reuse in CPUs.

As you may recall, shared memory is the fast, on-chip memory that can be accessed much faster than global memory. The size of the shared memory, which is local to each streaming multiprocessor, varies by Compute Capability and is generally very small compared to the size of the global memory. In certain situations, it's advantageous to keep frequently used values in shared memory, instead of relying on global memory and its local caches.

One of the most common examples of tiling is matrix multiplication. In a naive algorithm, the product matrix is calculated by performing dot products between the rows of the first matrix and the columns of the second matrix. Implementing this algorithm in CUDA is straightforward, as the kernel function can be configured to allow each thread to calculate one output element. This algorithm certainly works, but once you consider the memory access pattern of this code, you should notice that each element in the input matrices is accessed far too many times. For example, in a multiplication of two 4 × 4 matrices, each element of the input matrices is accessed 4 times, for a total of 4 × 4 × 4 × 2 global memory accesses. Even if most of these accesses are coalesced, fetching data from global memory can become the dominant cost for larger matrices. We will see that we can reduce the overall number of global memory accesses through the use of shared memory—and for large enough matrices, through tiling.

2×2 Matrix Multiplication

We will first look at the simplest possible case: how to reduce the number of global memory loads in a 2 by 2 matrix multiplication. In multiplying two such matrices A and B to form product C, A_0,0 is accessed when C_0,0 and C_0,1 are computed (as shown in blue in the figure below), and B_0,0 is accessed when C_0,0 and C_0,1 are computed (as shown in red in the figure). Thus, we see that each element of A and B must be accessed twice.

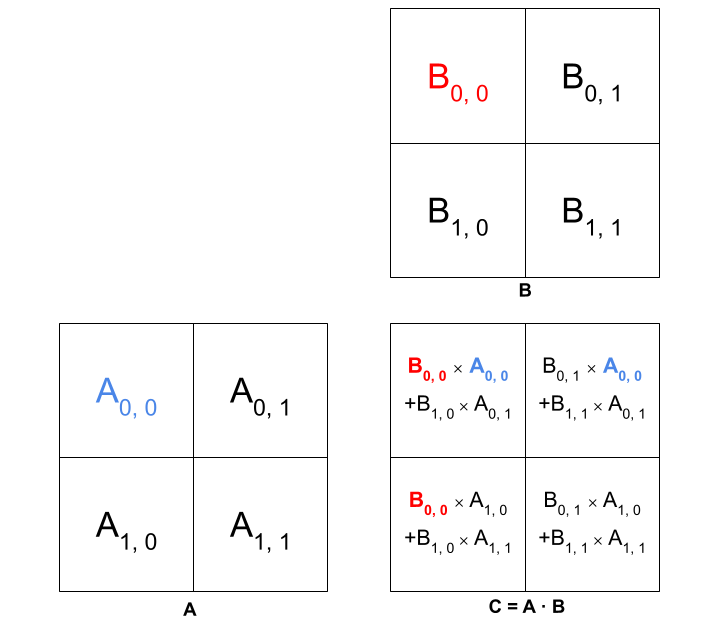
In the naive implementation of matrix multiplication, both accesses of each element of A and B are being done from global memory. However, if we load A and B into shared memory initially, then each element only needs to be accessed once from global memory; after that, further accesses are efficiently done through shared memory.

The use of shared memory is the key here. Let's assume that the threads are numbered like matrix elements. If thread_i,j loads the elements A_i,j and B_i,j into shared memory, the other threads are not prevented from accessing those elements. For example, elements A_0,0 and B_0,0 will be accessible not only to thread_0,0 but also to thread_0,1 and thread_1,0, so that all threads are able to compute their respective results. The same concept applies to every element in A and B.

The CUDA kernel below illustrates a shared-memory implementation of 2x2 matrix multiplication. Note that this strategy does require the use of a synchronization barrier, __syncthreads(), to ensure that A and B are fully loaded into shared memory before any accesses take place.

Notice that the indexing into A and B has been flattened for speed. Futhermore, tx correctly corresponds to the "fast" matrix dimension (i.e., the second index of C), so that memory accesses are coalesced. We see that the main goal has been accomplished: each element of A and B is loaded from global memory just once, then accessed twice through shared memory, reducing the number of times it's loaded from global memory. This improvement doesn't seem like much, so we will look at another example.

3×3 Matrix Multiplication

Now, we will apply the same concept to a 3×3 matrix. Each element of A and B needs to be accessed three times in this case. The three accesses of elements A_0,0 and B_0,0 are indicated by the blue- and red-colored triangles in the figure below.

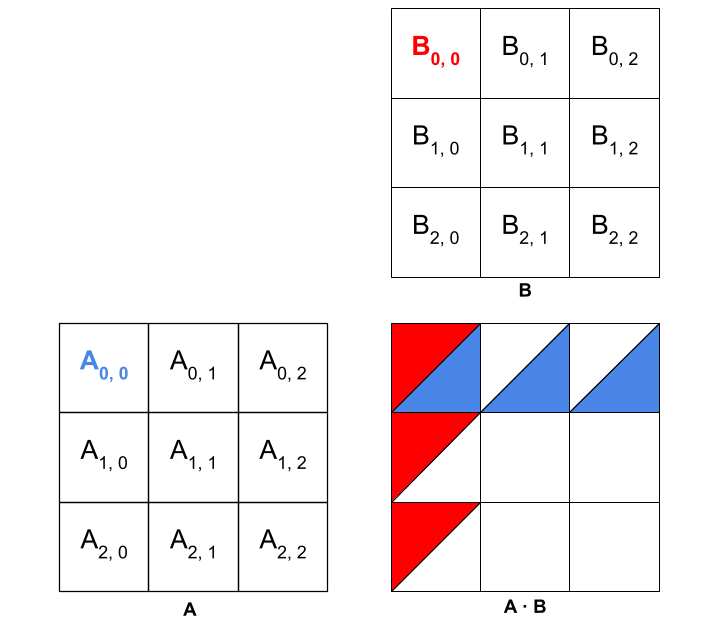
In a shared-memory implementation, thread_0,0 would still load A_0,0 and B_0,0 into shared memory, and so on, through thread_2,2. Thus, each thread is still doing only two loads from global memory, despite the change in matrix size. The 3 subsequent accesses of each element would all be done through shared memory.

Larger Matrices

As we increase the size of the matrices to a large dimension n×n, the number of global memory accesses remains at 2 per matrix element, instead of the 2n we would have in a naive implementation. Of course, the 2 intial accesses to global memory are followed by 2n shared-memory accesses for each element. However, the overall time for memory accesses becomes proportionally less, because an increasing fraction of the total accesses is done through shared memory.

But there are limitations to the approach outlined so far, because the scope of shared memory is just a single thread block. Once there are more than 1024 elements in A or B (i.e, once n>32), an implementation like the one above will not work, because CUDA limits the number of threads per block to 1024. Hence, larger matrices need to be divided into "chunks" that are correctly sized for a single block of threads. One block of threads, along with its associated "chunks" of memory, is called a tile. The size of a tile is not usually limited by the total size of shared memory: CUDA's shared memory generally holds at least 16k integers, enough to accommodate several blocks of threads at once.

We see now that the block-level restrictions are the real motivation for tiling in CUDA. Every block of threads must be able to define one set of tiles in shared memory and another set of tiles in the registers, such that neither set exceeds the limits set by the streaming multiprocessor. The optimal size of a block or tile will be specific to each computational problem. Typically, block sizes are based on multiples of 2 (e.g., 8×8, 16×16, 32×32) to maximize coalesced global memory loads during the first phase of tiling. Once the size of the blocks is chosen, the number of blocks, or the grid configuration, is automatically determined by the size of the output array.

Let's apply these ideas to the matrix multiplication problem. Clearly we will be working with submatrices of A and B, where each product of two submatrices accumulates into some submatrix of the final result.

As you can see in the figure above, the tile highlighted in green requires the blue and yellow highlighted elements from A and B. The shared memory that is allocated to the block of threads might not be enough to fit all the tiles from A and B that are required. Therefore, the threads associated with the green tile must load relevant submatrices from A and B, iteratively, in order to complete all the dot products that are required for the multiplication. The procedure is as follows:

• In the first iteration, the threads responsible for the shaded green elements load submatrix 1 from A and submatrix 1 from B and compute the required partial dot products between them. The partial sums can be stored in thread-local register variables.
• Next, the submatrices labeled 2 in this example are loaded from A and B, the dot products are computed, and the results are added to the partial sums in the same thread-local register variables. This completes the multiplication for the first submatrix of the product C (in this example).
• Concurrently, different blocks of threads are doing similar computations to fill in the other tiles of C.

In the general case, additional iterations may be needed; also, the the final submatrices taken from A and B may not be square. But in all cases, the threads in a given block proceed submatrix by submatrix, continuing along the rows of A and down the columns of B, until the iterations have covered all the elements needed from A and B for a given submatrix of C. This means that the kernel, which is run by each block, must have an outer loop that steps through submatrices of A and B. The number of iterations of this loop is simply the number of tiles across each axis. This CUDA kernel is sketched in the pseudocode below.

Note that a second __syncthreads() is introduced at the end of each iteration, so that the A and B tiles are not refreshed with new values until all the partial sums have been updated.

The tiling procedure modifies our original expectations. Collectively, the tiles are now performing two loads from global memory per element per iteration, because in each iteration each thread in the tile loads one element from A and one element from B in order to cycle all the required elements through shared memory by end of the iterations. Global-memory loads per thread thus become proportional to the number of tiles along one axis. Yet they are still less than those of the naive implementation, and this is what makes tiling in CUDA attractive.

The exercise on the next page presents a full, working CUDA code that contains two kernels, one with the naive implementation of matrix multiplication, and one with the tiling implementation. You can examine, compile, and run this code to see how tiling works in practice. In the exercise, there is one small weakness in the inner loop that calculates the partial dot products in the tiling implementation: some memory accesses are not coalesced and are likely to cause bank conflicts! Is this unavoidable? You can take that as a challenge!