Neighborhood collectives, introduced in MPI-3, provide a way to have implicit sub-communicators that are based on the existing topology. For instance, in the case of a Cartesian communicator, neighborhood communication simply involves the nearest neighbors in each direction, corresponding to rank_source and rank_dest in MPI_CART_SHIFT with input disp=1 for each dimension. Thus, the number of sources and destinations is 2*ndims (recall that ndims is specified in the call to MPI_CART_CREATE).

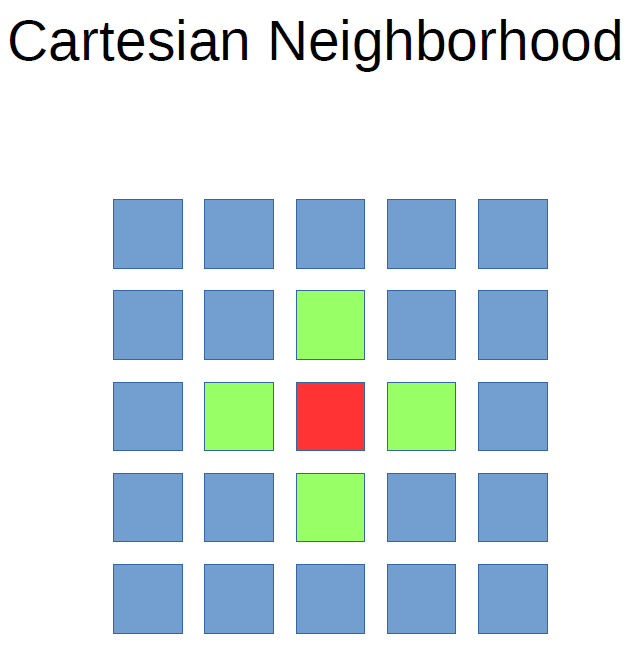
These "sub-communicators", called neighborhoods, are accessed through the use of neighborhood functions that are analogous to existing collective communication functions. Two processes are in the same neighborhood if they are linked by an edge, or if in Cartesian topology, all coordinates are the same except for possibly one coordinate, and the difference between the coordinates must be no more than one.

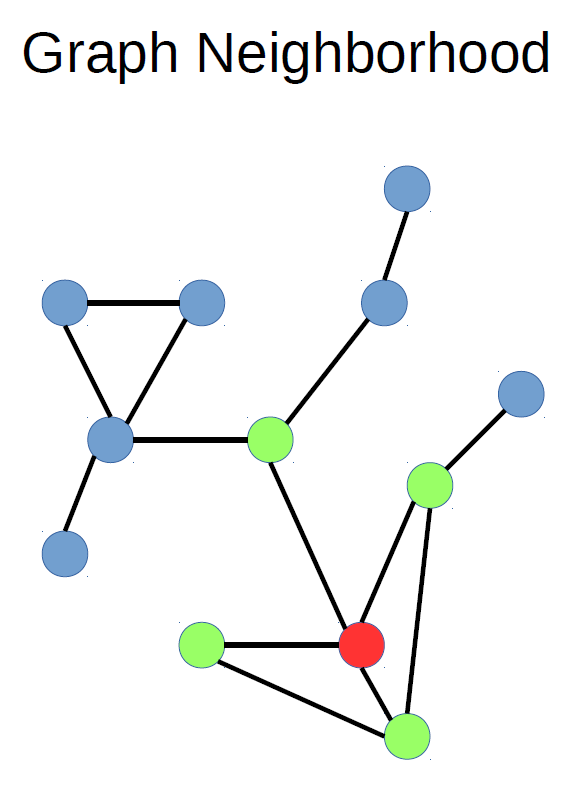
If an all-to-all MPI collective communication call has the name MPI_*, there is a corresponding neighborhood call MPI_NEIGHBOR_*. The precise meaning of the call depends on the type of topology, but the underlying theme is that each process communicates with its neighbors. As discussed in the topic about collective communications, MPI-3 introduced support for non-blocking variants of all collective communication calls. There are also non-blocking neighborhood variants for these calls, and if the name of the blocking variant is MPI_*, the non-blocking neighborhood variant is MPI_INEIGHBOR_*.