Neural networks are flexible computational models that can process inputs and produce outputs, with parameters that can be fit or estimated based on data. They represent a type of computational graph inspired by the action of neurons in the brain. The structure of these models reflects a directed network of artificial "neurons" or nodes, in which data are presented as inputs to a network, those inputs are fed through the neural network architecture — which includes one or more hidden layers — and which ultimately produces outputs. This general architecture is represented schematically in the left panel of the figure below. It is conventional to represent neural networks as flowing from left to right, with the input nodes on the far left and the output nodes on the far right. Within the illustration of an entire neural network, we highlight a subset of nodes and edges in red.

Just as the network as a whole includes a set of inputs and outputs, so does each individual node in the network, as illustrated in the right panel of the figure below. Each edge that connects two nodes carries with it an associated weight, indicating the strength of influence between the two nodes. In the network depicted below, for each node \(j\) in layer \(k+1\), a set of incoming inputs \(x^k_j\) are multiplied by the corresponding weights \(W^k_{i,j}\) along each edge, and those products are summed. Finally, a bias or offset \(b_j\) is added to the sum to define an aggregated, weighted input for that node. Computationally, this is accomplished as a matrix-vector multiplication involving the weight matrix \(\bar W^k\) and the node vector \(\vec x^k\), followed by the addition of the bias vector \(\vec b^k\). The value of that node \(x^{k+1}_j\) is computed by applying an activation function \(f\) to the aggregated input. That output \(x^{k+1}_j\) then serves as an input to downstream nodes in the network. The right panel of the figure below illustrates this action for one node in the network, but all other nodes in the network are updated simultaneously in an analogous manner, each with its own set of inputs and edge weights. Inputs are mapped through all the internal (hidden) layers of the network until an output is produced at the end.

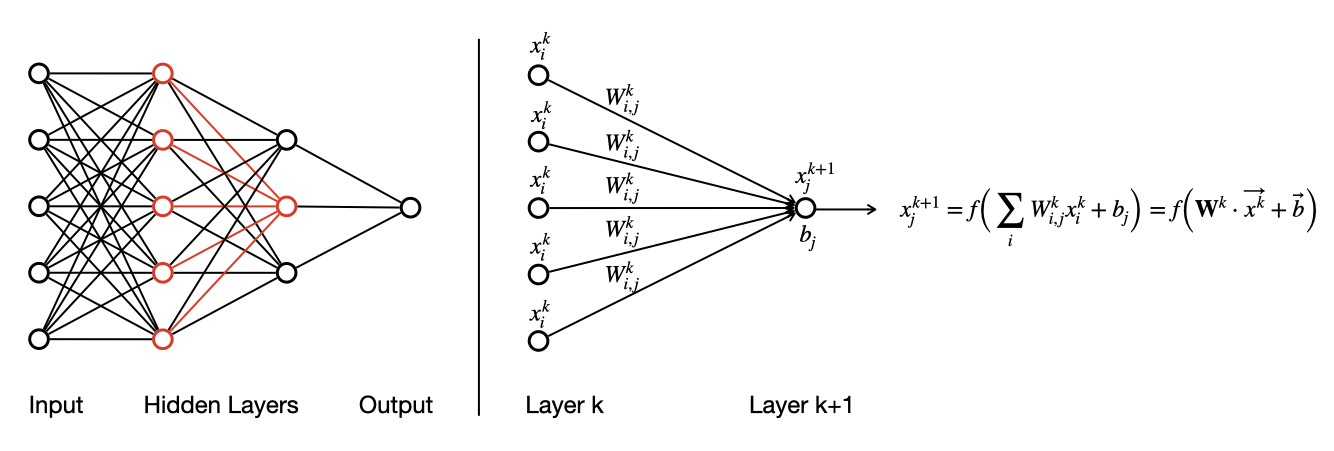
The action of the network is parameterized by the edge weights \(\bar W\) and the biases \(\vec b\). Depending on the numerical values of those parameters, the outputs computed by the network, for a given set of inputs, can vary. The "learning" that is at the core of deep learning is the determination of suitable values for those numerical parameters that do a good job of producing a mapping (function) between the inputs and the outputs. One property that makes neural networks very powerful in this task is that they are universal functional approximators: with a sufficient number of nodes, a neural network can approximate any sufficiently smooth function that maps inputs to outputs. This learning process is described in more detail on the next page.

In a supervised learning problem, each input has associated with it a corresponding label or value that is to be learned by the network. The input layer encodes the data elements that are to be trained on, and the output layers produce the predictions of the associated labels or values. The job of the learning algorithm is to tune the parameters of the neural network to do a good job of associating inputs with outputs, and doing so in a generalizable fashion so that it can make accurate predictions about labels associated with new data that have not been trained on. In an unsupervised learning problem, patterns in data are to be learned, without any explicit labels on the data. These patterns might consist of clusters of similar data points or a reduction to a lower dimensional space that allows for easier interpretation. One common approach for unsupervised learning using deep learning is to construct an autoencoder that compresses the inputs to a lower-dimensional space and then attempts to reconstruct the original data using that lower-dimensional representation. Structure detected in the lower-dimensional embedding space can serve as a useful summary of patterns in the original data.

Designing an appropriate network architecture for a given problem is itself an art and a science, the details of which are beyond the scope of this tutorial. For certain classes of problems, however, there are architectural elements that are regularly used, such as convolutional layers for image processing applications and transformer architectures for large language models. In the page on Models and Predictions, we describe these in the context of models trained on large datasets.