We've seen the significant performance penalty that can be incurred due to cache misses. The cost motivates us to avoid writing code that has large strides, or that causes a single cache line to be shared across different threads. However, we can go beyond merely avoiding cache misses and aim for cache reuse, where we try to use data not just once but multiple times after they are brought into cache. An important example of this is array blocking, sometimes called loop tiling. The idea is to partition large arrays into chunks that fit entirely within one level of cache while operations on these chunks are being conducted.

The classic case for using array blocking comes from matrix-matrix multiplication. First, let's look at an obvious, naive way to code this operation:

By definition, each entry in the product matrix c requires an entire row and column from the matrices being multiplied. When this is coded naively, as above, it means that at least one matrix will always be accessed along its "bad" direction (along a row, in this Fortran example). Additionally, since each row of a and column of b is used n times, there might be as many as n repeated fetches of both matrices in their entirety, using the naive matrix multiply approach. That is a significant performance hit, and it motivates us to see if there might be some better way to define the memory layout for this operation.

Let's look instead at a blocked or tiled matrix-matrix multiply. The outer trio of loops defines the blocks, and the inner trio of loops accesses the entries within those blocks:

This technique is also called loop tiling because we fetch sub-matrices or tiles of a and b and perform partial dot products (sums) over the tiles, accumulating the partial sums into the appropriate tiles of the product matrix c. After all the tiles of a and b have been computed, the product matrix c is complete.

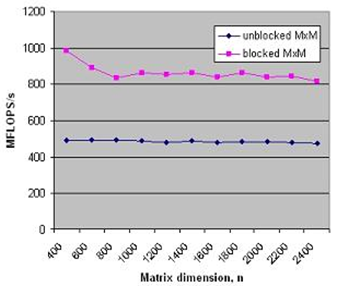
Provided we make the tiles or blocks small enough so that all three fit together into cache at the same time, each block of a and b will be fetched only one time. Once we've done this for all blocks, we've accumulated the entire sum for each entry in the matrix c. As we can see below (from tests on an older processor model), making the extra effort to implement array blocking can lead to significant speed improvements, even for moderately large matrices.

In technical terms, array blocking enhances performance by improving the code's computational intensity as well as its data locality. What this means in plain language is that the code can do more floating-point operations per main-memory access, and the data are brought closer to where they are needed for doing these operations.

Evidently, in order to optimize nontrivial matrix operations, you may be grappling with issues that are more subtle than making sure a couple of nested loops are ordered correctly. Perhaps array blocking seemed straightforward to implement in the illustration above, but in the general case the best block size will depend on the exact cache capacity and other hardware details, as well as the nesting structure of the loops. The real takeaway from all of this is that you should not even bother writing code to do standard matrix operations; you can just call performance libraries that have already figured out all the best techniques for matrices of all sizes.

The principles of cache awareness are nevertheless good to know because they are applicable in other contexts. For example, when processes use MPI to communicate, the inter-process bandwidth increases greatly if the messages fit entirely within cache. Resizing MPI messages based on cache considerations can be called data tiling, which is obviously similar to loop tiling.