It is important to understand a few details of how the processor's hardware fetches items from the main memory into the L1 data cache, because this turns out to have implications for codes in which a large stride is for some reason unavoidable.

When we discussed the memory hierarchy previously, we saw that each core of an SKX processor in Stampede2 holds 32 KB of data in its local L1 cache, for a total of 768 KB of data across all the L1 caches of the 24 cores in the processor. (The 32 KB refers only to the L1d cache, i.e., the portion of the L1 that stores data; each core also includes an L1i cache for storing instructions, adding another 32 KB to the local L1.) The L1 data cache is further divided into segments called cache lines, whose size represents the smallest amount of memory that can be fetched from other levels in the memory hierarchy. The size of a cache line is 64 bytes in Skylake.

The most flexible cache arrangement is termed fully associative. This means that a fetched line can land anywhere in cache. But searching for a particular line in this arrangement tends to be slow. The opposite extreme, found in Intel KNL processors, is direct-mapped cache. This means that a fetched cache line has only one place to go, so that searching for a particular line is fast. But this scheme runs the risk of under-utilization of cache, resulting in more frequent access collisions. Intel Skylake, like most processors, employs a compromise: n-way associative cache, where 1 < n < # cache lines. This means that a given physical address in the main memory may be fetched into one of n possible locations in the cache.

The 32KB of L1 data cache in an SKX core can therefore be envisioned as a three-dimensional box, where:

• Depth (into the page) represents the size of a cache line, e.g., 64 bytes in Skylake
• Height represents the extent of a cache set (to be discussed)
• Width represents the number of sets that are available

After doing a few quick calculations, we can find the relevant properties for the L1d cache of an SKX core, which holds 32 KB divided into 64-byte cache lines and is 8-way set associative:

• Bytes in L1d = 32 KB * 1024 (bytes/KB) = 32768 bytes
• Cache lines in L1d = 32768 / (line size) = 32768 / 64 = 512
• Number of sets = 512 / 8 = 64.

This leads to the following diagram, in which the depth has been flattened:

Recall that each square above represents an entire cache line (64 bytes in our case). When data at a particular address is requested, the congruence class of the address is computed, determining the cache set of the cache line containing the data. Then the entire line is fetched into one of the eight slots for that cache set. This illustration shows (in green) which slots are available for a cache line that contains a particular address, if the address happens to be mapped to class number 6:

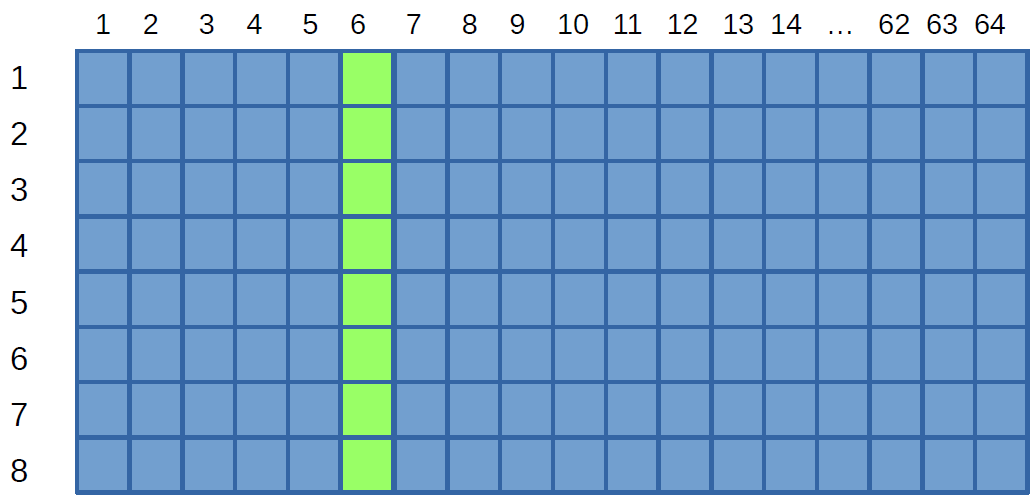
But how does the mapping occur? Each address is divided into three parts: tag, index, and offset. The index identifies the congruence class and the corresponding cache set (the "column" that the cache line can be fetched into):

The tag and the index are used to find the particular cache line, and the offset gives the address of the byte of interest within the cache line.¹

Because the L1 cache is structured in this way, we see that bad things will happen when data are accessed with a stride that is a multiple of a large power of 2. In terms of the above diagram, the worst case arises when the stride is equivalent to one complete row, or a multiple of it, because successive fetches will then belong to the same congruence class (same index). This effectively shrinks the size of the L1d cache from 32KB to just 8 cache lines, or 512 bytes! Specifically, such a scenario occurs when the stride is equal to m*(#indexes)*(cache line size) = m*64*64 bytes = m*4096 bytes (m >= 1). When this occurs, at most 8 addresses will be read in at a time, possibly resulting in highly frequent fetches from slower parts of memory. This is called cache thrashing.

With this knowledge in mind, it can be helpful to do your own padding to avoid strides with large powers of 2. This can come up in matrices where the major dimension is a large power of 2, a size which might be favored if FFTs are being applied along rows or columns, e.g. Embedding a matrix that is a large power of 2 within a slightly larger matrix is usually fairly straightforward to do, with just a little knowledge of linear algebra.

^{1. For those familiar with hash functions in computer science, cache line look-up is an example of a hash function. In this case, the hash function is the truncation of the left part and right parts of the address to get the index. Once the index is known, the tag is used as the key to look up the cache line of interest. ^}