Matrix multiplications lie at the heart of Convolutional Neural Networks (CNNs). Both training and inferencing require the multiplication of a series of matrices that hold the input data and the optimized weights of the connections between the layers of the neural net. The Tesla V100 is NVIDIA's first product to include tensor cores to perform such matrix multiplications very quickly. Assuming that half-precision (FP16) representations are adequate for the matrices being multiplied, CUDA 9.1 and later use Volta's tensor cores whenever possible to do the convolutions. Given that very large matrices may be involved, tensor cores can greatly improve the training and inference speed of CNNs.

The Tesla V100 has 640 tensor cores in total: there are 8 in each of its 80 SMs, arranged so that one SM's 4 processing blocks hold 2 apiece. A single tensor core can perform 64 half-precision FMA operations per clock cycle, so that the 8 tensor cores in one GV100 SM can perform 512 FMAs (1024 individual floating point operations!) per clock cycle.

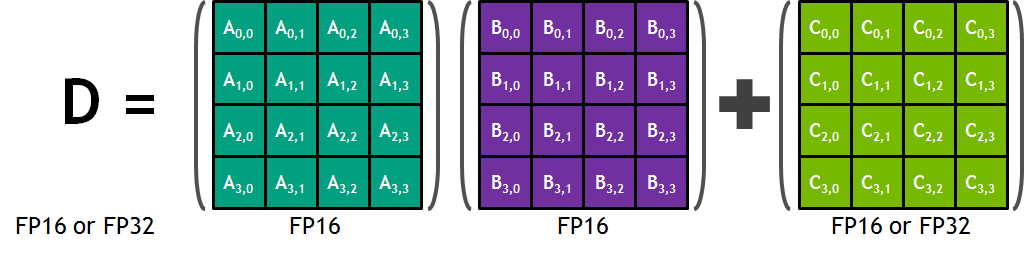
The basic role of a tensor core is to perform the following operation on 4x4 matrices:

\[ \text{D} = \text{A} \times \text{B} + \text{C} \]

In this formula, the inputs A and B are FP16 matrices, while the input and accumulation matrices C and D may be FP16 or FP32 matrices (see the figure below).

NVIDIA has come up with a way to visualize the action of the tensor core in 3D, which is shown in the next figure. However, this illustration isn't easy to understand at a glance. Here is an attempt to describe in words what it aims to illustrate, namely, how the tensor core performs fully parallelized 4x4 matrix operations.

The two matrices to be multiplied, A and B, are depicted outside the central cube (note, matrix A on the left is transposed). The cube itself represents the 64 element-wise products required to generate the full 4x4 product matrix. Imagine all 64 blocks within the cube "lighting up" at once, as pairs of input elements are instantaneously multiplied together along horizontal layers, then instantaneously summed along vertical lines. As a result, a whole product matrix (A times B, transposed) drops down onto the top of the pile, where it is summed with matrix C (transposed), outlined in white. Upon summation it becomes the next output matrix D and is pushed down onto the stack of results. Prior output matrices are shown piling up below the cube, beneath the latest output matrix D (all transposed).

The reality of how the tensor core works is undoubtedly much more complicated than the illustration suggests. Probably it involves a multi-stage FMA pipeline that progresses downward layer by layer. One then envisions successive C matrices dropping in from the top to accumulate the partial sums of the products at each layer.