The most common measure of scalability is called speedup. It is the ratio of time to complete the problem on one PE (processing element—which can be a node, processor, or core), versus time to complete the problem on N PEs. If 32 PEs finish in 1/32 the time, then the speedup is 32, which is considered perfect or linear speedup. If they finish faster than that, it is called super-linear speedup. Super-linear speedup can happen when breaking a problem into more pieces makes all the pieces execute more efficiently. For instance, maybe one whole piece becomes small enough to fit into the cache of a single core.

Based on speedup S, there are several ways to define scalability. The most straightforward way measures how S varies with N for a fixed problem size. This is called strong scaling. It means that on N processors, your code is able to solve a given problem N times faster than it does on one processor (or nearly so); it comes close to linear speedup. In this scenario, your program takes the same input and divides the work among more processors, so that each one works on a smaller chunk, without loss of efficiency. If the problem takes twenty minutes on 64 nodes, then it should take ten minutes on 128 nodes.

There's always a catch

But a simple analysis shows there’s a catch, which has come to be known as Amdahl's Law. The program's main algorithm might parallelize nicely, but there is always some portion of time spent saving to disk, sending to the network, or performing some calculation that must be done identically on all of the nodes. In our model, we call this serial time, whereas the parallelizable part of the calculation is called the parallel time. For N PEs,

\[total~time = serial~time + {parallel~time\over N} = s + {p \over N}\]

Speedup is the ratio of the above expression for N=1 and N>1; after some manipulation this becomes

\[speedup = {N\over1+(N-1)a}, where~a = {s\over{s+p}}\]

For large N, this expression doesn't asymptote at N, but at a constant, 1/a, which equals 1 over the serial fraction of the work.

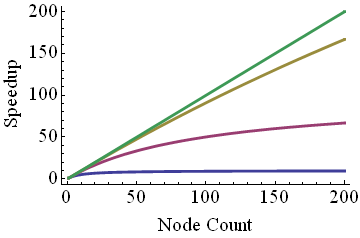
The nasty asymptote occurs because as you increase the number of PEs to infinity, the total time doesn't go to zero but to the serial time. Even worse, if the (parallel time)/N is already smaller than the serial time, then throwing more PEs at the problem doesn't help much. It is an inefficient use of resources, so you, and the other users of this system, will be better off if you run your jobs at a smaller core count.

It looks like strong scaling is pretty tough to achieve, but it's not the only way to define scalability. In fact, it may not be all that relevant to what you and many other researchers would like to do with a machine like Frontera. Why? Because you might not be trying to do the same work faster; you might want to do more work without waiting longer. If that's the case, then you have a different path to good scalability.