Two Ways to Scatter
Example of two ways (simple way, better way) to do a scatter.
Simple approach
One process scatters the N messages to the other processes, one at a time.
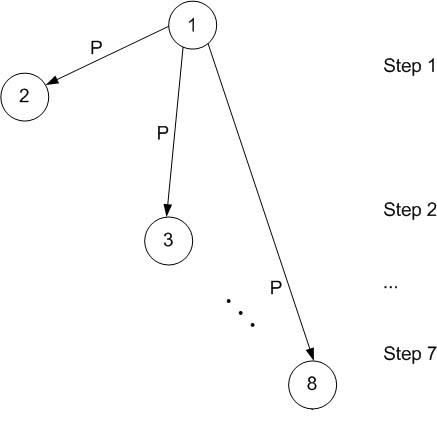
| Amount of data transferred | \((N-1)*p\) |
|---|---|
| Number of processes | \(N\) |
| Size of message | \(p\) |
| Number of steps | \(N-1\) |
Smarter approach
Let other processes help propagate the message. In the first step, process 1 sends half of the data (size 4*p) to process 2. In the second step, both processes can now participate: process 1 sends the half of the data it kept in step 1 (size 2*p) to process 3, while process 2 sends one half of the data it received in step 1 to process 4. At the third step, four processes (1, 3, 2, and 4) are sending the final messages (size p) to the remaining four processes (5, 6, 7, and 8).
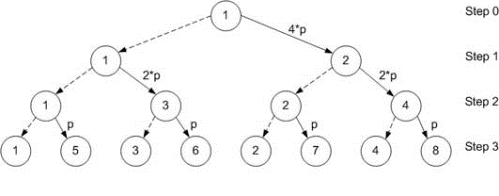
| Amount of data transferred | \(\log_2 N * N * p/2\) |
|---|---|
| Number of processes | \(N\) |
| Size of message | \(p\) |
| Number of steps | \(\log_2 N\) |
Compare the number of steps in the two approaches:
- Simple approach: \(N-1\)
- Smarter approach: \(\log_2 N\)
In terms of operations, the latter scales better as N increases.
The tree propagation optimizes the number of operations at the expense of increased data transfer. For very large message sizes, there is clearly redundancy in data transfer using this second approach, so bandwidth limitations should be considered in such cases. It may not be a problem if enough parallel network paths are available.