Dataset operations are identified by the prefix H5D. A dataspace is a persistent property of a dataset; HDF5 dataspace operations are denoted by the H5S prefix.

Create / Open

hid_t H5Dcreate( hid_t f_id, const char *fname, hid_t d_id, 
                 hid_t s_id, hid_t lcpl_id,
                 hid_t dcpl_id, hid_t dapl_id )

hid_t H5Dopen( hid_t f_id, const char *fname, hid_t dapl_id )

Read and Write

herr_t H5Dread( hid_t d_id, hid_t memtype_id, 
                hid_t memspace_id, hid_t filespace_id, 
                hid_t xplist_id, void *buf )

herr_t H5Dwrite( hid_t d_id, hid_t memtype_id,
                 hid_t memspace_id,  hid_t filespace_id, 
                 hid_t xplist_id, const void *buf )

Hyperslabs

herr_t H5Sselect_hyperslab( hid_t s_id, H5S_seloper_t op, 
                            const hsize_t *start, 
                            const hsize_t *stride, 
                            const hsize_t *count, 
                            const hsize_t *block )

H5Sselect_hyperslab() is used to select a subset of the dataspace (hyperslab) to add to the currently selected region for the dataspace identified by s_id. The op parameter is used to perform a logical operation on the current selection such as H5S_SELECT_SET, H5S_SELECT_AND, and so on. The parameters start, stride, count, and block indicate the offset to the start of hyperslab, hyperslab stride, number of blocks, and block size respectively, in each dimension of the hyperslab. Essentially these parameters define the hyperslab selection. Note that start, stride, count, and block are all arrays, and they must have the same size as the dimension of the dataspace. If we consider a 3D dataspace, then the parameters should be 1D arrays of size 3, where each array element represents a value in the corresponding dimension.

A typical usage of a hyperslab in parallel is as follows:

• Each process calls H5Sselect_hyperslab() to define memory and file hyperslabs.
• Each process executes a read/write call using the hyperslabs defined. The type of MPI-IO call (independent or collective) is defined by the data transfer property list set prior to the read/write calls.
• The hyperslab parameters define the portion of the dataset to be written.

The following figure illustrates how hyperslab-based I/O works using contiguous and chunked writes (or reads) in parallel. Note that hyperslabs can also be defined for writing into (or reading from) a file in parallel using different patterns, such as regularly spaced data and checkerboard patterns.

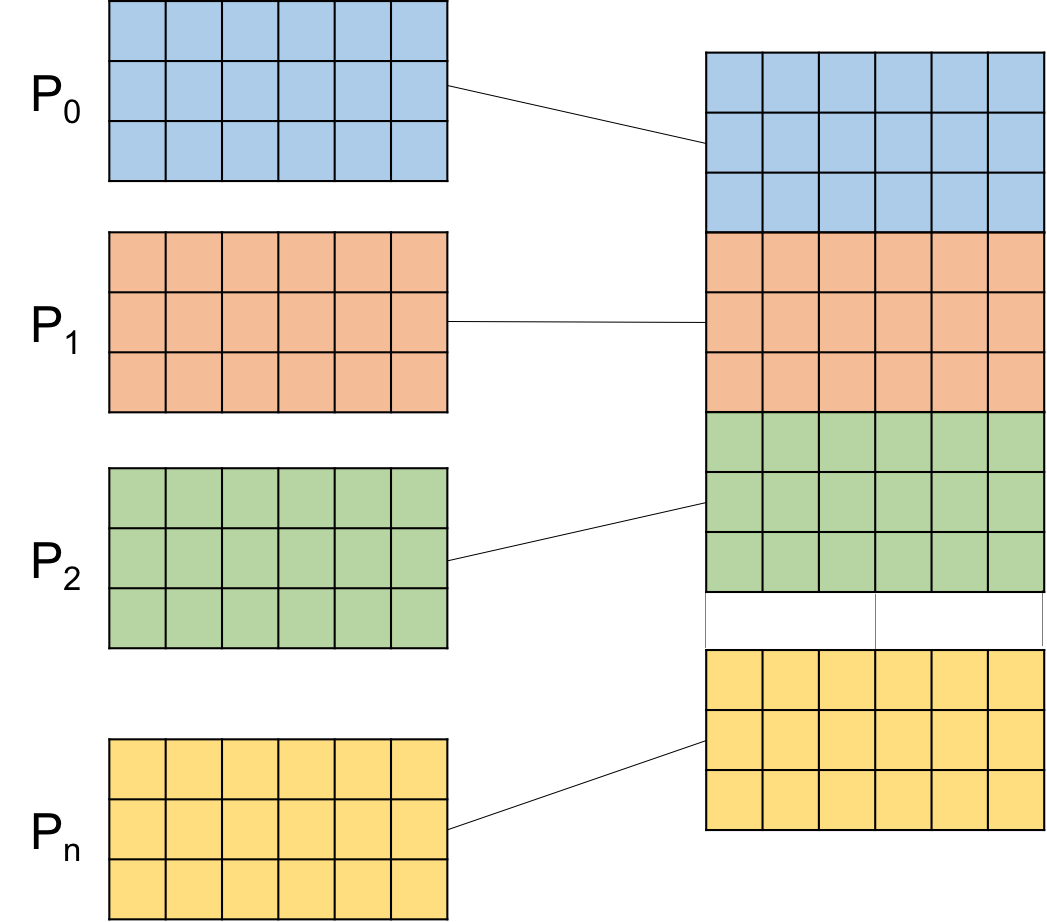
In this example, n processes are writing contiguous hyperslabs into a file in parallel. The dataset dimension is dimx by dimy, or here, 12 by 6 (assuming n = 4). As the dataset is two-dimensional, each of the parameters start, stride, count, and block is an array of 2 elements. The following are the values of these parameters:

count[0] = dimx/4; count[1] = dimy;
start[0] = rank*count[0]; start[1] = 0;
stride[0] = 1; stride[1] = 1;  //It can be passed NULL (default)
block[0] = 1; block[1] = 1;   //It can be passed NULL (default)

The second figure illustrates a non-contiguous mapping of the dataspace to four processes.

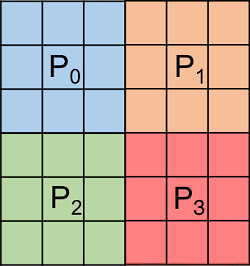
In this example, four processes write chunked hyperslabs, each of dimension 3x3. The following are the values of the parameters:

count[0] = 1; count[1] = 1;
switch(P) {
    case 0 : start[0] = 0; start[1] = 0; break;
    case 1 : start[0] = 0; start[1] = 3; break;
    case 2 : start[0] = 3; start[1] = 0; break;
    case 3 : start[0] = 3; start[1] = 3; break;
}
stride[0] = 1; stride[1] = 1;  // It can be passed NULL (default)
block[0] = 3; block[1] = 3;