Cornell Virtual Workshop > MPI Collective Communications > Data Movement

Gather/Scatter Effect

In order to illustrate the gather and scatter functions, we give a matrix-style depiction below:

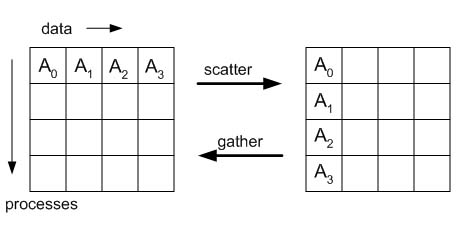
A matrix representation of gather/scatter, where rows represent the processes and columns represent the data. Before the operation, the data is on the root process. Scattering the data sends a specific portion of the data array to each process, so that the data is distributed across processes. Gathering the data returns the distributed data to the root (or designated) process, restoring the initial state of the matrix. — Matrix illustration of gather/scatter.

Let's consider in detail how MPI_Gather might be used to facilitate a distributed matrix computation.

Example: matrix-vector multiplication

Matrix is distributed by rows (i.e., row-major order)
Product vector is needed in entirety by one process
MPI_Gather will be used to collect the product from processes

Description of Sample Code

The problem associated with the following sample code is the multiplication of a matrix A, size 100x100, by a vector b of length 100. The example uses four MPI processes, so each process will work on its own chunk of 25 rows of A. Since b is the same for each process, it will simply be replicated across processes. The vector c will therefore have 25 elements calculated by each process; these are stored in cpart. Here is a picture of how the overall computation is distributed:

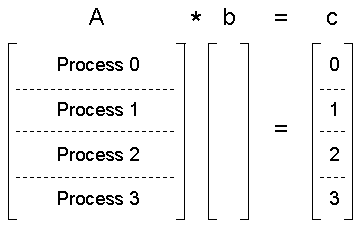
Matrix-vector multiplication visualized as described in text — Matrix-vector multiplication.

A: a matrix partitioned across rows and distributed to processes as Apart
b: a vector present on all processes
c: a partitioned vector updated by each process independently

The MPI_Gather routine will retrieve cpart from each process and store the result in ctotal, which is the complete vector c.

MPI_Gather Example

/* Compute a partition of matrix A multiplied by vector b */
float Apart[25,100], b[100], cpart[25], ctotal[100];
int root;
root=0;
⋮
/* Code that initializes Apart and b */
⋮
for(i=0; i<5; i++)
{
   cpart[i]=0;
   for(k=0; k<100; k++)
   {
      cpart[i] = cpart[i] + Apart[i,k] * b[k];
   }
}
MPI_Gather(cpart, 25, MPI_FLOAT, ctotal, 25, MPI_FLOAT,
    root, MPI_COMM_WORLD);

! Compute a partition of matrix A multiplied by vector b
! Fortran, unlike C, stores matrices in column-major order,
! so for speed, each submatrix of A is stored as its transpose, ApartT
REAL ApartT(100,25), b(100), cpart(25), ctotal(100)
INTEGER root
DATA root/0/
⋮
! Code that initializes ApartT and b
⋮
DO I=1,25
     cpart(I) = 0.
     DO K=1,100
          cpart(I) = cpart(I) + ApartT(K,I) * b(K)
     END DO
END DO
CALL MPI_GATHER(cpart, 25, MPI_REAL, ctotal, 25, MPI_REAL, &
      root, MPI_COMM_WORLD, ierr)

Back