Let's start with something familiar and build our intuition.

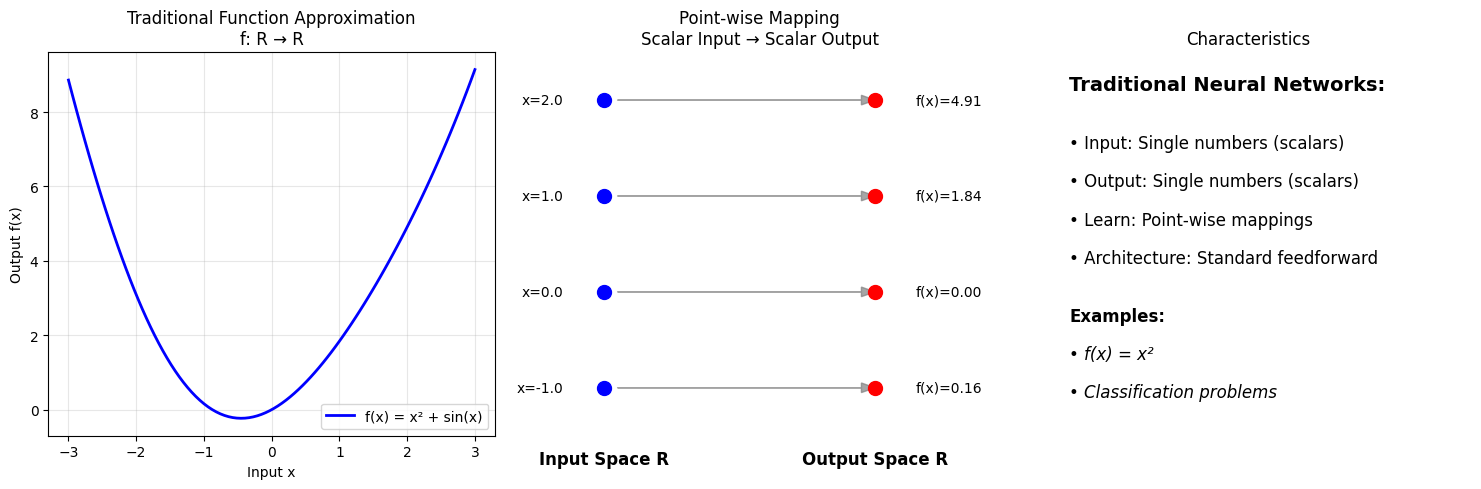
Traditional Function Approximation

We know neural networks can learn mappings like:

• Input: A number \( x = 2.5 \)
• Output: A number \( f(x) = x^2 = 6.25 \)

This is point-wise mapping: each input point maps to an output point.

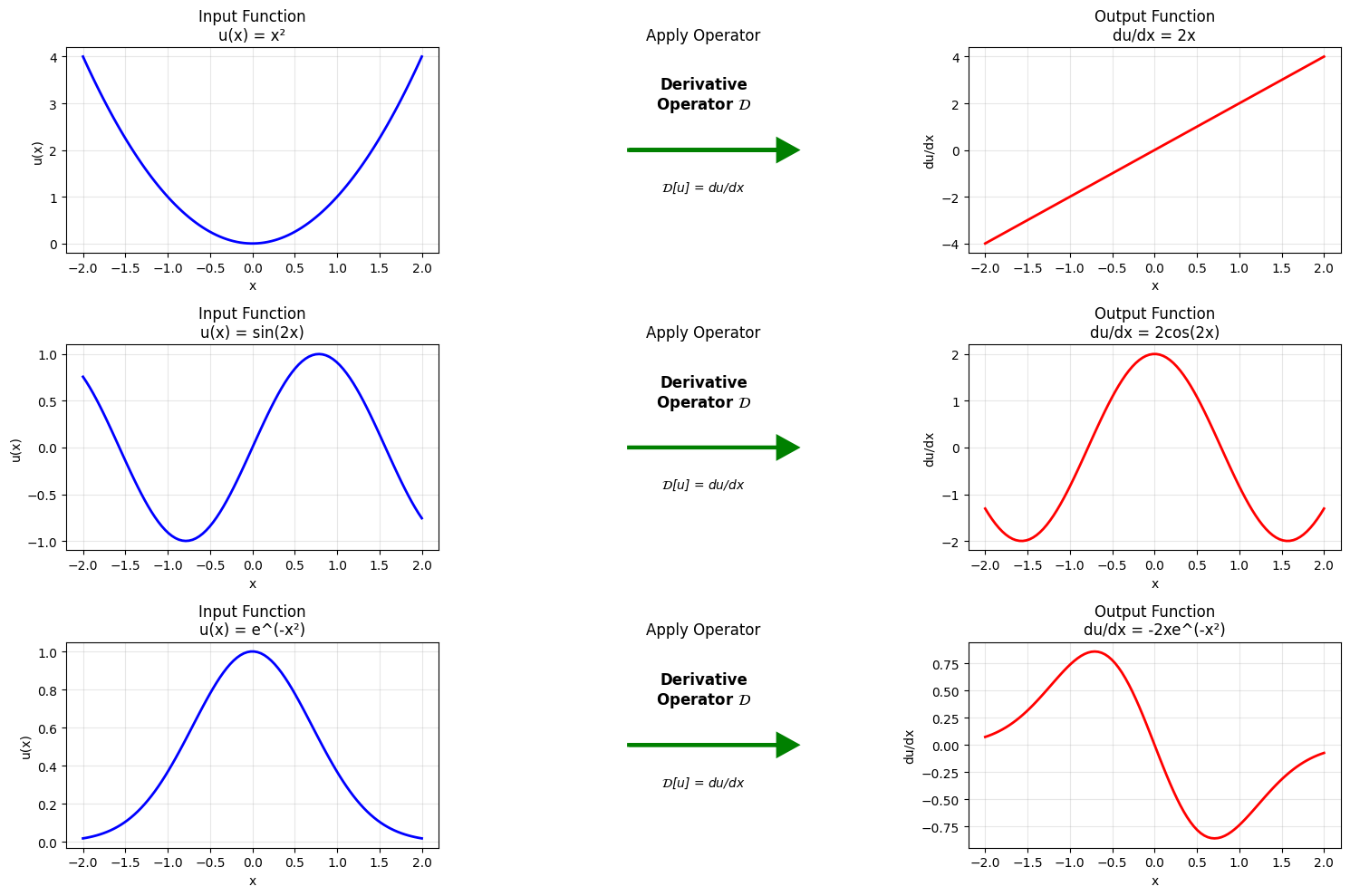
Operator Learning: The Next Level

Now imagine:

• Input: An entire function \( u(x) = \sin(x) \)
• Output: Another entire function \( \mathcal{G}[u](x) = \cos(x) \) (the derivative!)

This is function-to-function mapping: each input function maps to an output function.

Examples of operators we encounter in science:

1. Derivative operator: \( \mathcal{D}[u] = \frac{du}{dx} \)
2. Integration operator: \( \mathcal{I}[f] = \int_0^x f(t) dt \)
3. PDE solution operator: Given source \( f \), return solution \( u \) of \( \nabla^2 u = f \)

Operator Learning