Mathematical Formulation

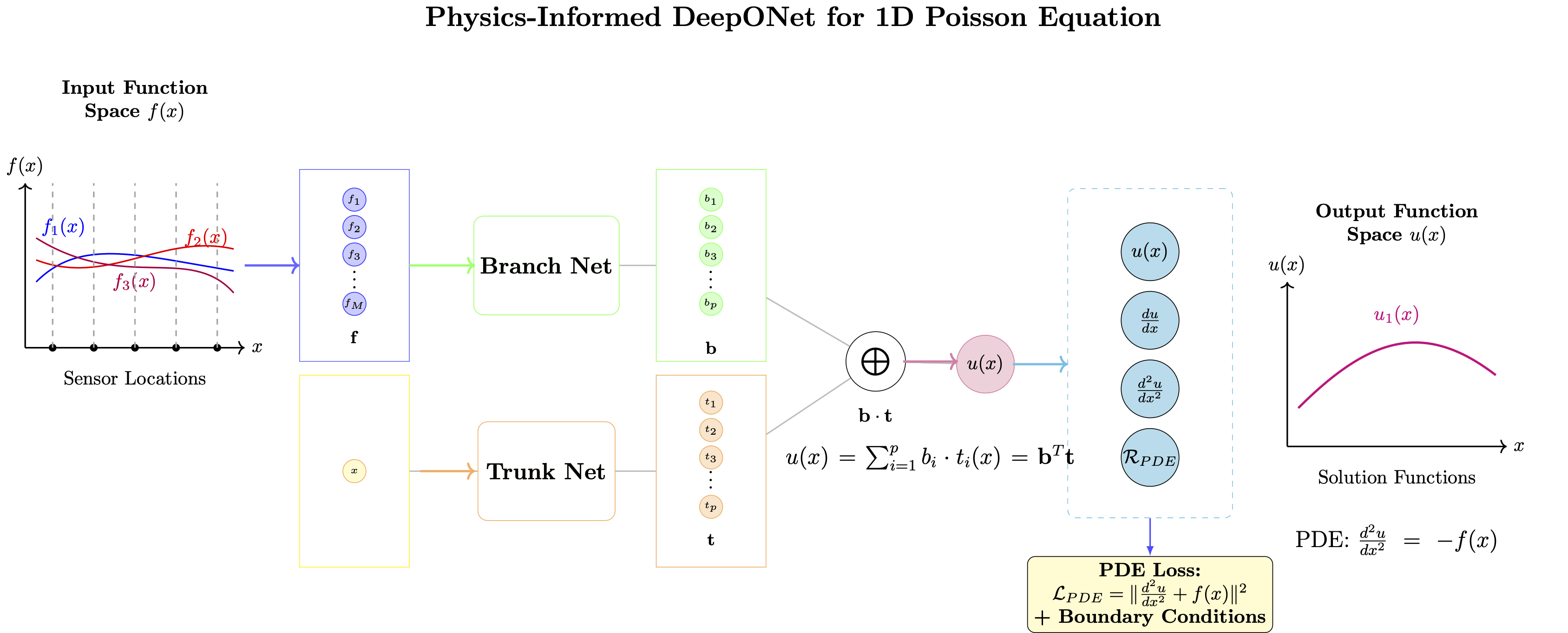
We want to learn the solution operator \( \mathcal{G} \) that maps source functions \( f(x) \) to solutions \( u(x) \):

where \( u(x) \) satisfies:

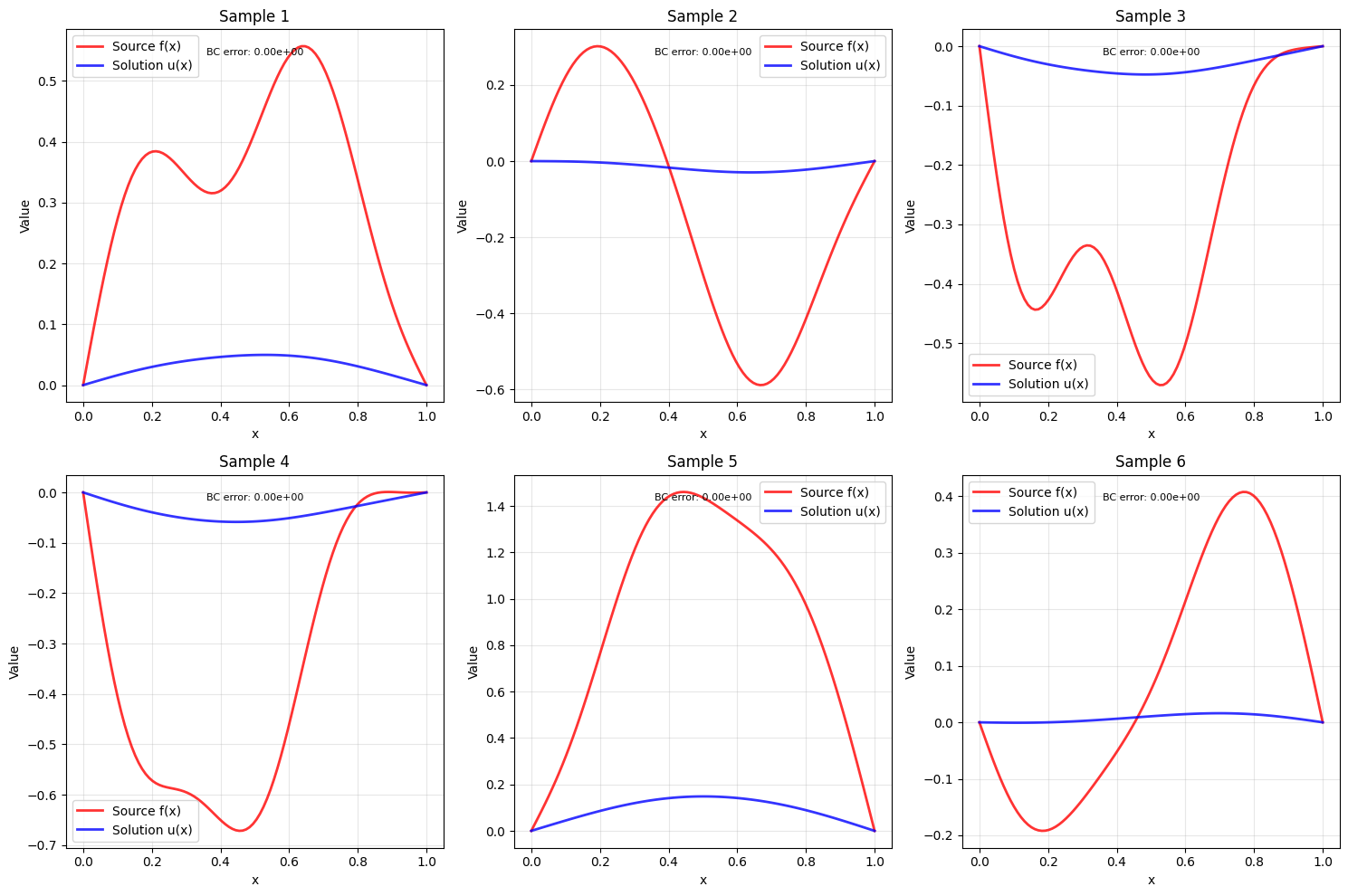
• PDE: \( \frac{d^2u}{dx^2} = -f(x) \) for \( x \in [0,1] \)
• Boundary conditions: \( u(0) = 0 \), \( u(1) = 0 \)

Physics-Informed Loss Components

1. Data Loss: \( \mathcal{L}_{data} = \frac{1}{N} \sum_{i=1}^N \|u_{pred}^{(i)} - u_{true}^{(i)}\|^2 \)
2. Physics Loss: \( \mathcal{L}_{physics} = \frac{1}{N} \sum_{i=1}^N \left\|\frac{d^2u_{pred}^{(i)}}{dx^2} + f^{(i)}\right\|^2 \)
3. Boundary Loss: \( \mathcal{L}_{boundary} = \frac{1}{N} \sum_{i=1}^N \left[|u_{pred}^{(i)}(0)|^2 + |u_{pred}^{(i)}(1)|^2\right] \)
4. Total Loss: \( \mathcal{L} = \mathcal{L}_{data} + \lambda_{physics} \mathcal{L}_{physics} + \lambda_{boundary} \mathcal{L}_{boundary} \)