Perfect starting point: Learn the derivative operator \( \mathcal{D}[u] = \frac{du}{dx} \)

Why this example:

• Simple and intuitive
• Exact analytical solution for verification
• Shows how DeepONet learns basis decompositions
• Bridges function approximation → operator learning

Problem Setup

Input functions: Cubic polynomials \( u(x) = ax^3 + bx^2 + cx + d \)

Target operator: \( \mathcal{D}[u](x) = \frac{du}{dx} = 3ax^2 + 2bx + c \)

where \( w_1 = c \), \( w_2 = 2b \), \( w_3 = 3a \).

The DeepONet challenge: Can it learn this mapping automatically?

Data Generation for DeepONet

Key Concept: We're learning the derivative operator \( D[u] = du/dx \)

• For cubic polynomials \( u(x) = ax^3 + bx^2 + cx + d \)
• The derivative is \( u'(x) = 3ax^2 + 2bx + c \)

Data Generation

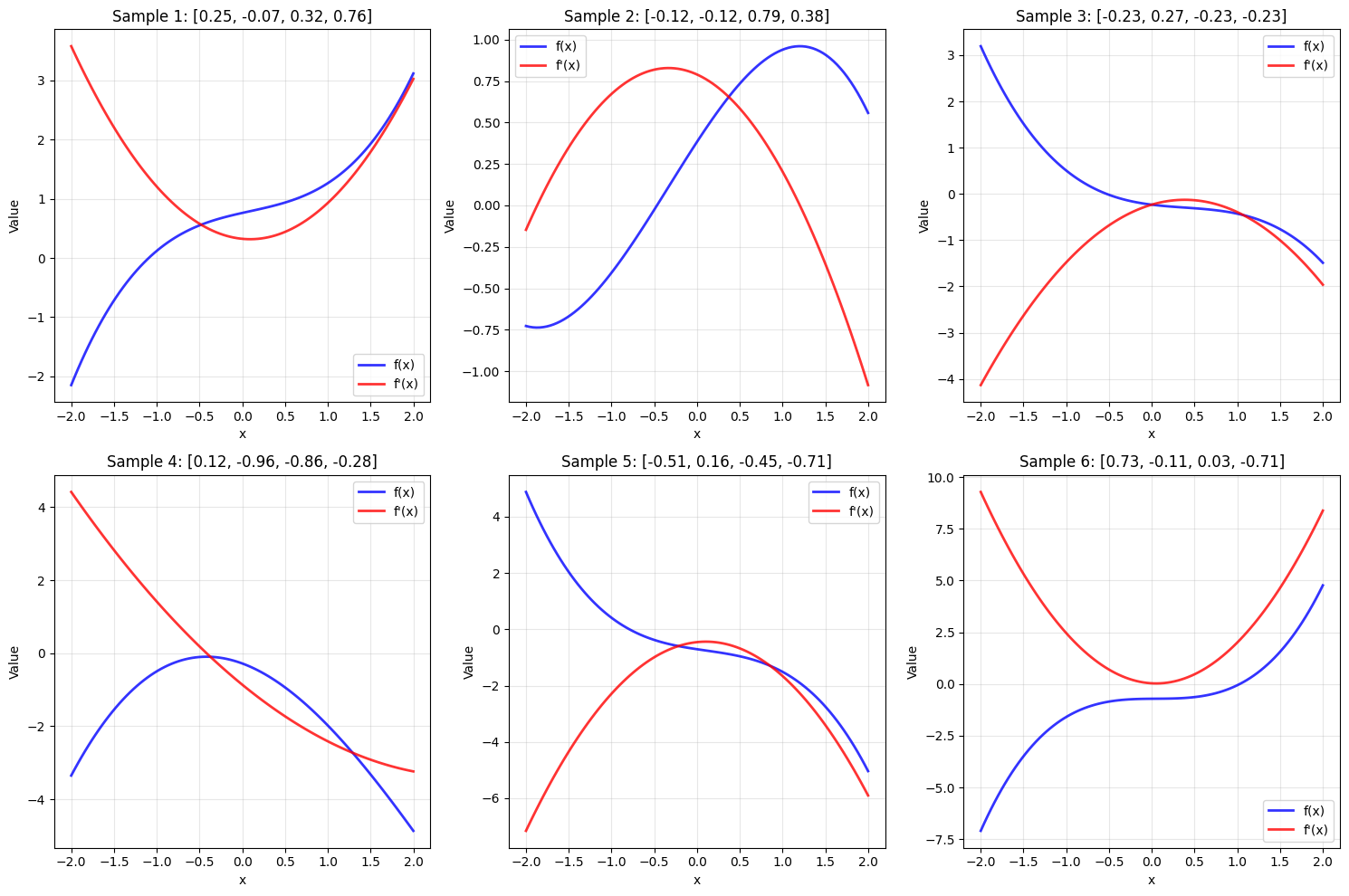
DeepONet Implementation

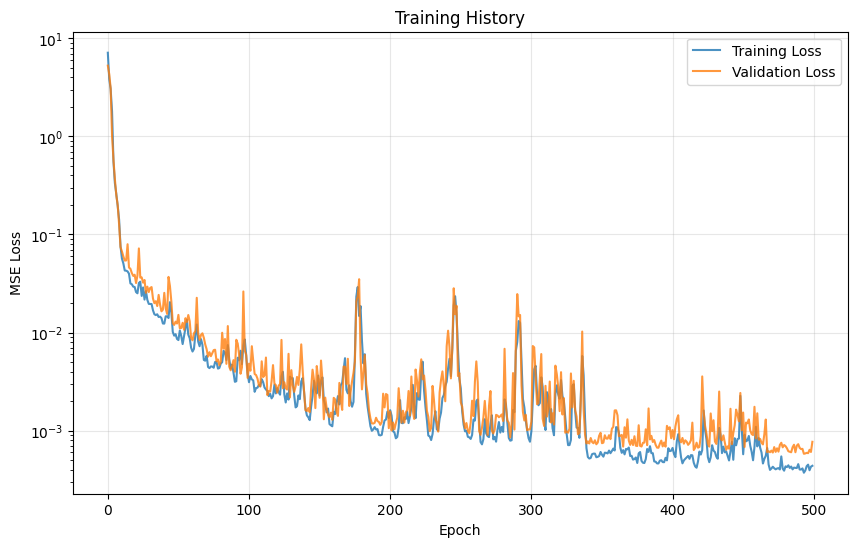
Training

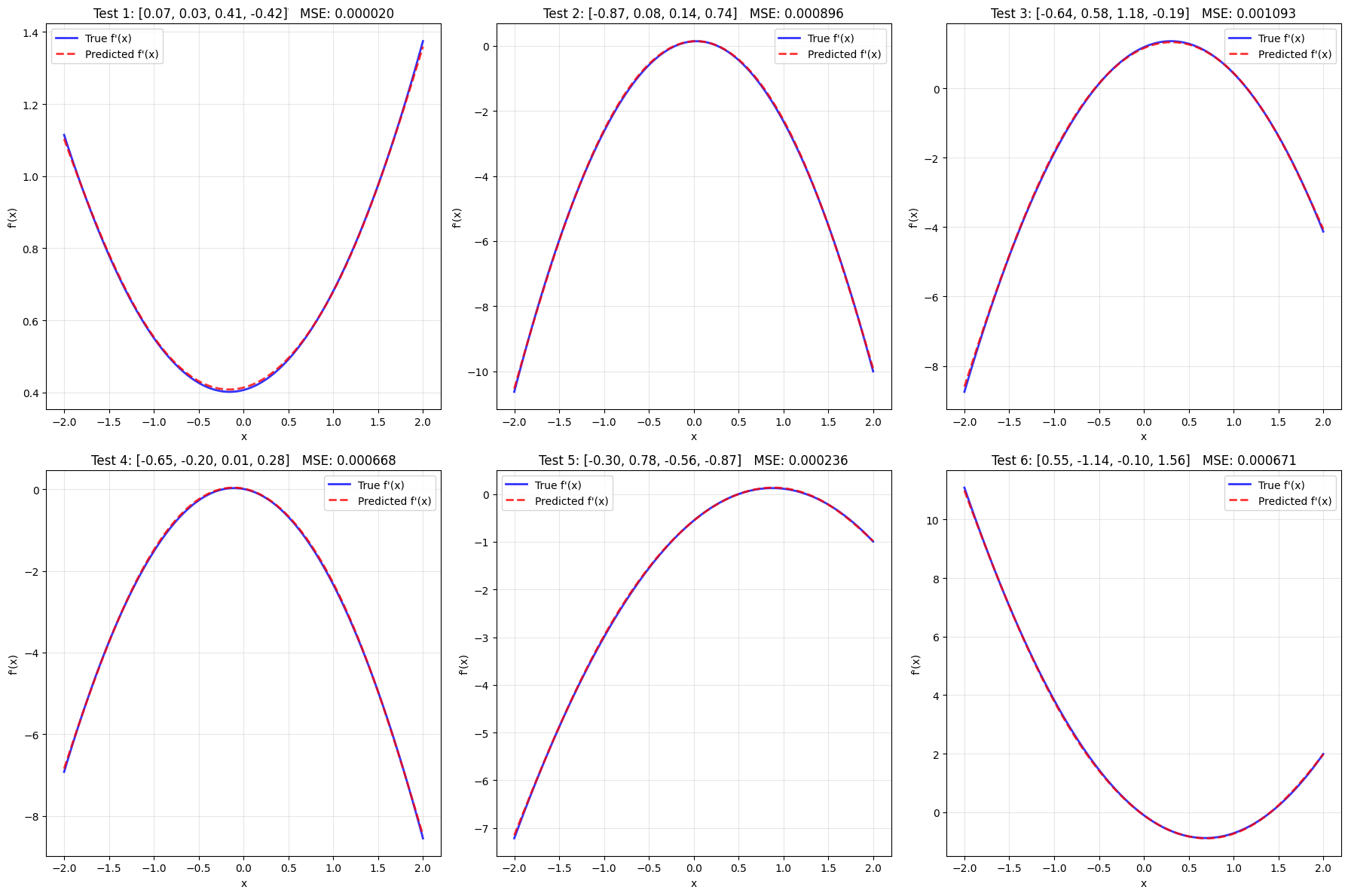
Evaluation of model

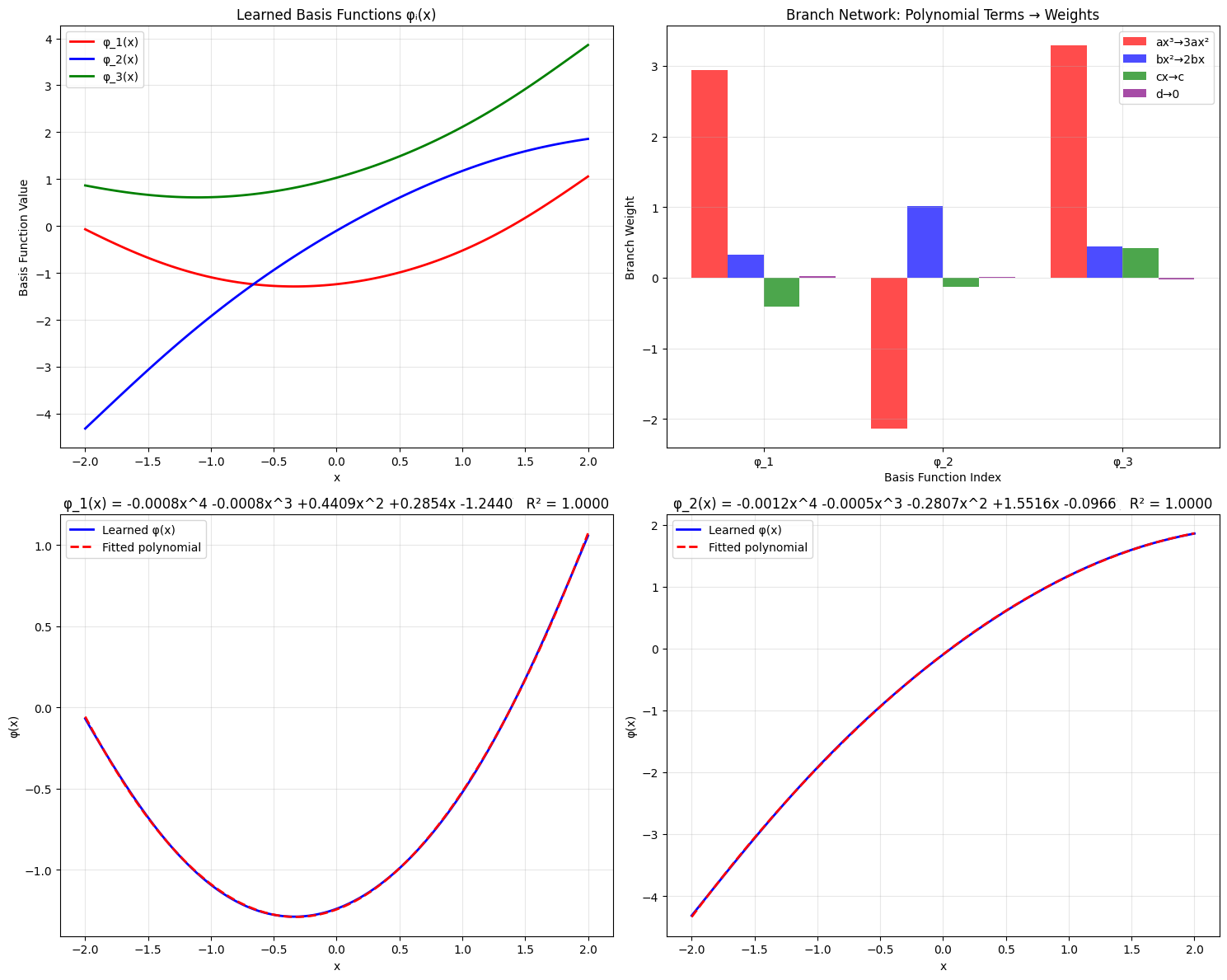
Understanding What DeepONet Learned

Critical question: Did DeepONet truly learn the derivative operator, or just memorize patterns?

Let's test it on completely new types of functions it has never seen!