Multi-Layer Perceptron
Physics-Informed Neural Networks (PINNs)
DeepONet: Operator Learning with Neural Networks
Differentiable Simulation
Graph Neural Network
Lab Setup

The 1D Nonlinear Darcy Problem

Now for something more challenging: A real PDE with nonlinear physics!

Problem Formulation

The 1D nonlinear Darcy equation models groundwater flow with solution-dependent permeability:

\[ \frac{d}{dx}\left(-\kappa(u(x))\frac{du}{dx}\right) = f(x), \quad x \in [0,1] \]

where:

  • u(x) is the solution field (e.g., pressure or hydraulic head).
  • The \( \kappa(u) \): is non-linear solution-dependent permeability is κ(u(x)) = 0.2 + u²(x).
  • The input term f(x) is a Gaussian random field defined as f(x) ~ GP(0, k(x, x')) such that k(x, x') = σ² exp(-||x - x'||² / (2ℓ_x²)), where ℓ_x = 0.04 and σ² = 1.0.
  • Homogeneous Dirichlet boundary conditions u(0) = 0 and u(1) = 0 are considered at the domain boundaries.

The Operator Learning Challenge

Goal: Learn the solution operator \( \mathcal{G} \) such that:

\[ \mathcal{G}[f] = u \]

where \( u \) is the solution to the nonlinear Darcy equation for source \( f \).

Key insight:

This is much harder than the derivative operator because:

  1. Nonlinear PDE: No analytical solution
  2. Random sources: Infinite variety of input functions
  3. Complex physics: Solution depends on entire source profile

Why This Matters

Traditional approach: For each new source \( f \), solve the PDE numerically (expensive!)

DeepONet approach: Learn the operator once, then instant evaluation for any new source

Let's examine the existing Darcy implementation

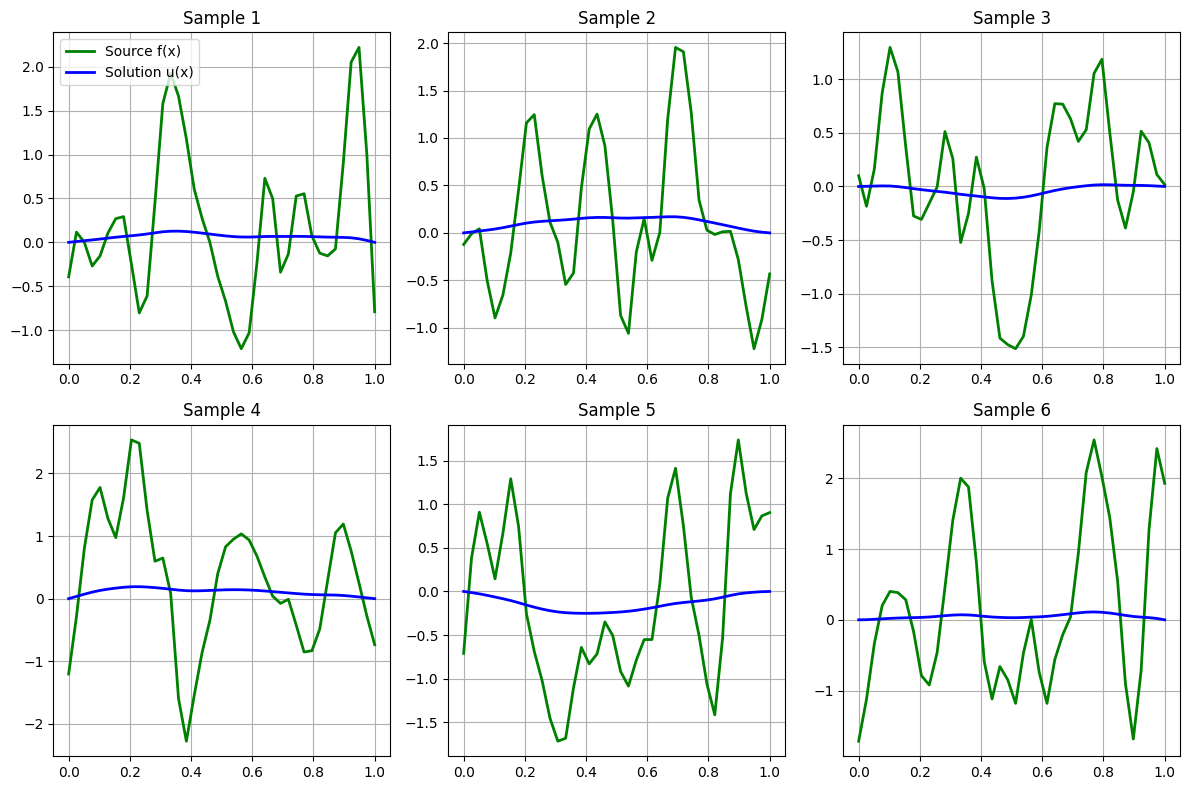
DeepONet Architecture

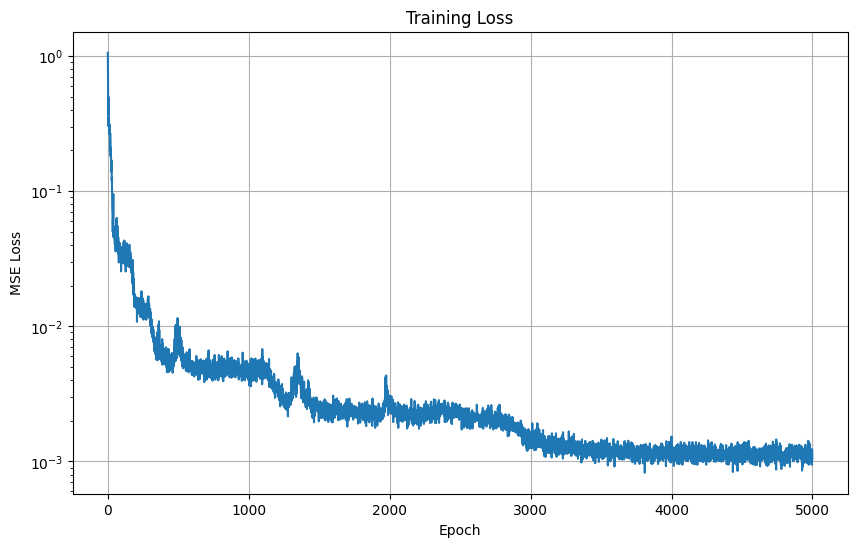
Training

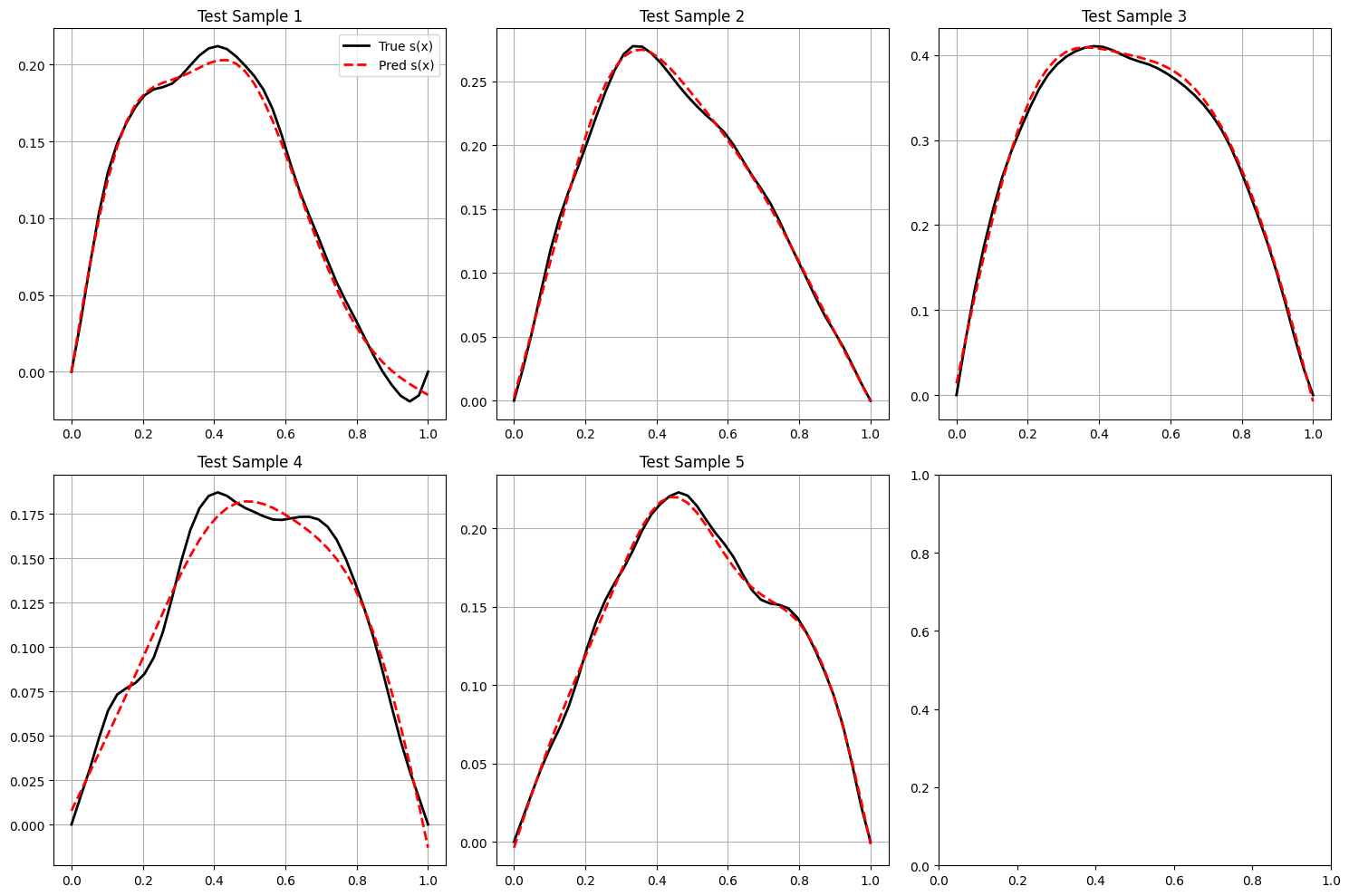
DeepONet Prediction

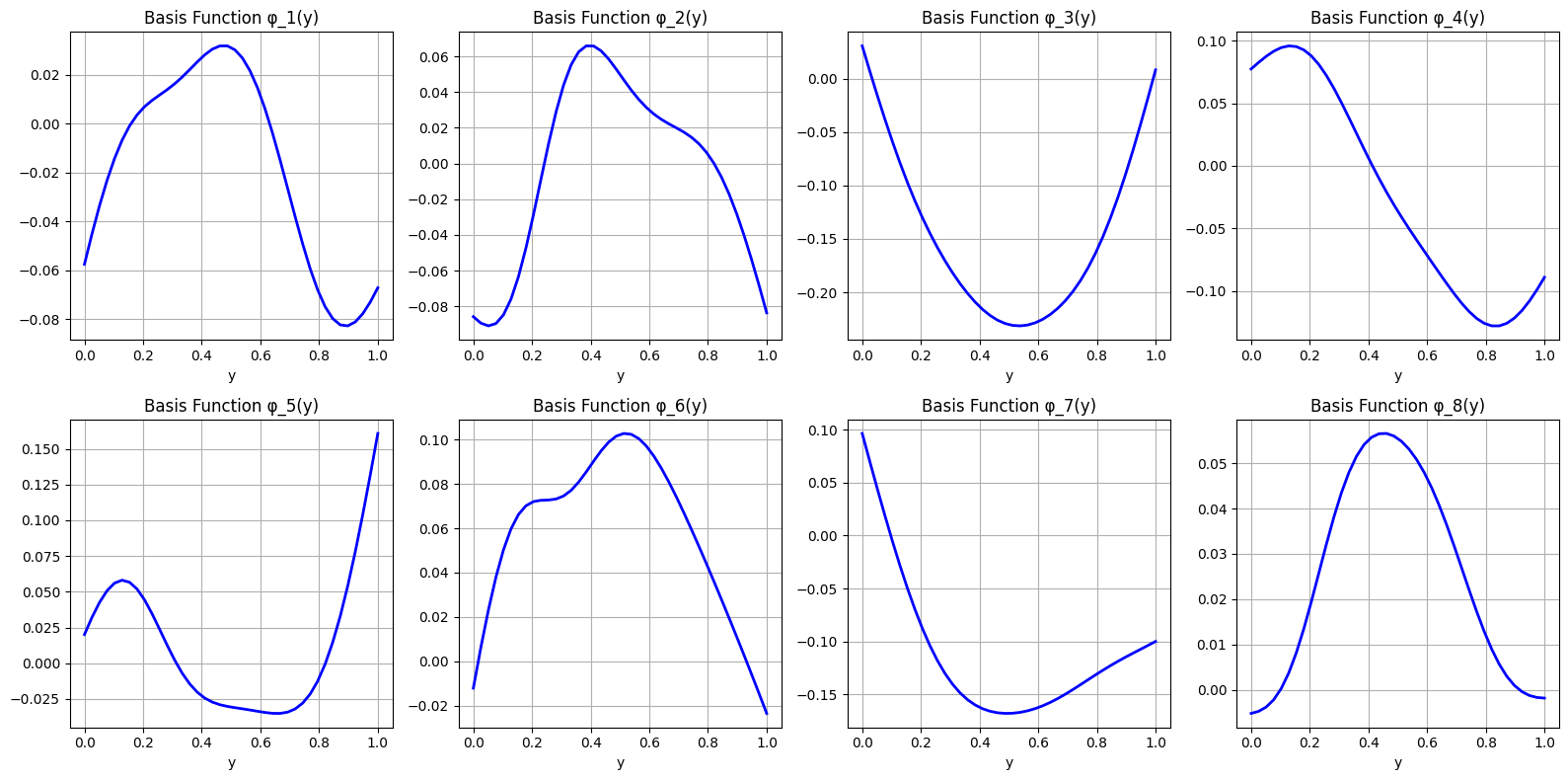
Understanding basis functions

Back
 
Next
©  |   Cornell University    |   Center for Advanced Computing    |   Copyright Statement    |   Access Statement
CVW material development is supported by NSF OAC awards 1854828, 2321040, 2323116 (UT Austin) and 2005506 (Indiana University)