Image Classification and CNN
Building a CNN Classifier with PyTorch: Part 1
Building a CNN Classifier with PyTorch: Part 2
Introduction to DDP with PyTorch
Single Node Multi-GPU Training with torchrun
Multi-node Distributed Training with PyTorch
Lab Setup

Multi-Layer Perceptron (MLP)

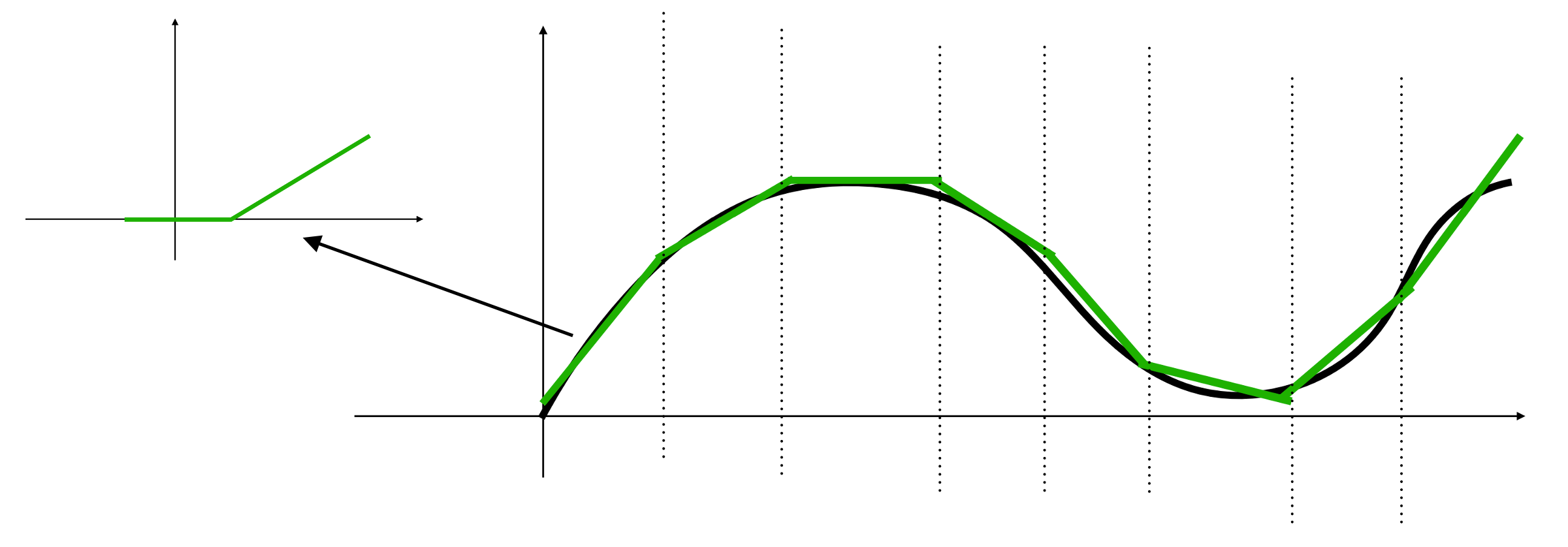
When MLP is applied to a linear regression problem, it can be considered as building a piecewise linear function to simulate the target curve.

piecewise linear function to simulate the target curve

Layers in MLP are called linear layers or fully connected layers. Neurons in each layer are fully connected to the neurons in the following layer. The Figure below shows an example of MLP for binary classification.

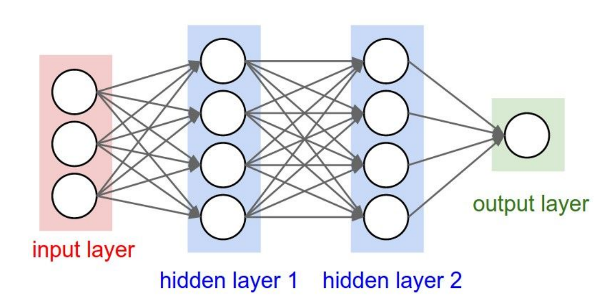
piecewise linear function to simulate the target curve
Deep Learning
Image source: [1]

Here are some terminologies for a MLP:

\(w^{(i)}\): weight matrix of layer \(i\)
\(o^{(i)}\): output of layer \(i\)
\(x\)​: input vector
\(y\): output scalar
\(\sigma\): activation function (e.g. sigmoid, ReLu)

Here is the formula for the MLP shown in the figure:

\(o^{(1)} = \sigma((w^{(1)})^Tx)\)
\(o^{(2)} = \sigma((w^{(2)})^To^{(1)})\)
\(y = (w^{(3)})^To^{(2)}\)

For binary classification (i.e. dataset has only two possible labels), we can define one class with label 1 and the other class with label -1, and then use the sign of \(𝑦∈\mathbb{R}\) as the classification result. For multiclass classification, we use one output per class that uses the softmax activation function.

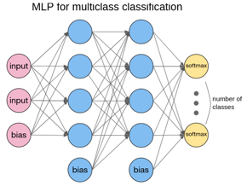
MLP for multiclass classification
Deep Learning
Image source: [2]
References:
Back
 
Next
© Chishiki-AI  |   Cornell University    |   Center for Advanced Computing    |   Copyright Statement    |   Access Statement
CVW material development is supported by NSF OAC awards 1854828, 2321040, 2323116 (UT Austin) and 2005506 (Indiana University)