Training and Testing
Training is the process of making a model. The training data is data “observed” by the learning model. Testing is the process of evaluating the performance of the model. The testing data is data NOT "observed" by the learning model. Once a model is trained, we can make predictions by applying the model to data not in either training or testing data set. We assume the input data and the predictions are produced from the same process for all training data.
A basic idea in training machine learning models is to minimize a loss function. Numerical optimization methods like gradient descent are commonly used to find optimal values for the parameters \(w\). At every iteration, gradient descent tweaks the parameters to minimize the loss function \(L\). Below is the math describing the process of gradient descent:
Backpropagation is used to calculate the gradient of the loss function with respect to weights. Fortunately, manual derivation for gradients of different neural networks is not needed. All modern ML/DL frameworks (e.g. PyTorch and Tensorflow) have an automatic differentiation engine, which is usually implemented based on backpropagation through a computation graph.
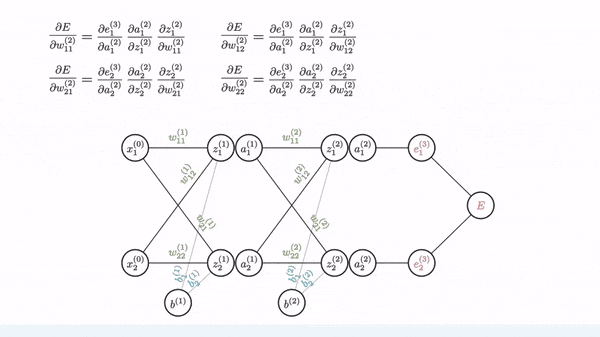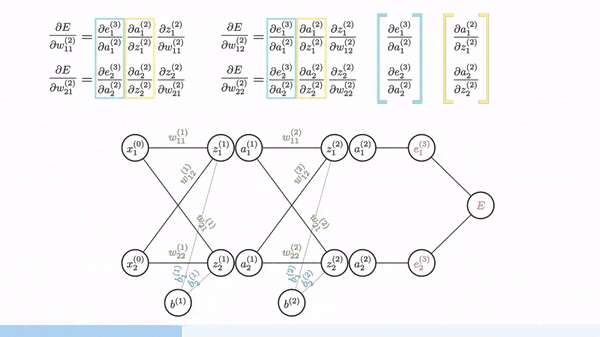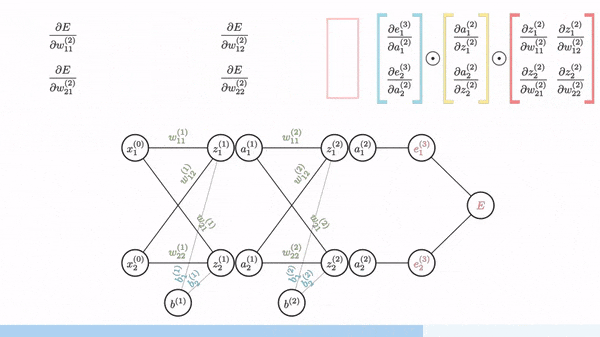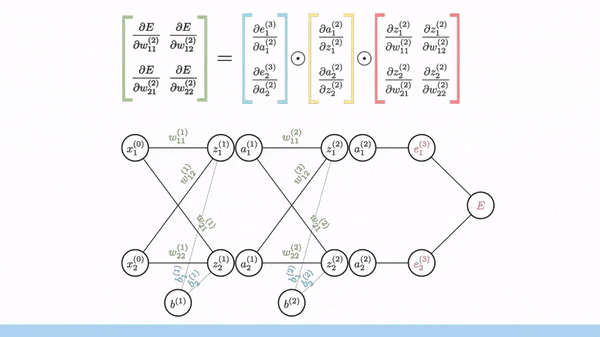
Image source: [1]
CVW material development is supported by NSF OAC awards 1854828, 2321040, 2323116 (UT Austin) and 2005506 (Indiana University)