Activation functions are applied element-wise to the output of a linear transformation within a neuron or layer. They introduce the non-linearity required for neural networks to learn complex mappings.

Some common activation functions include:

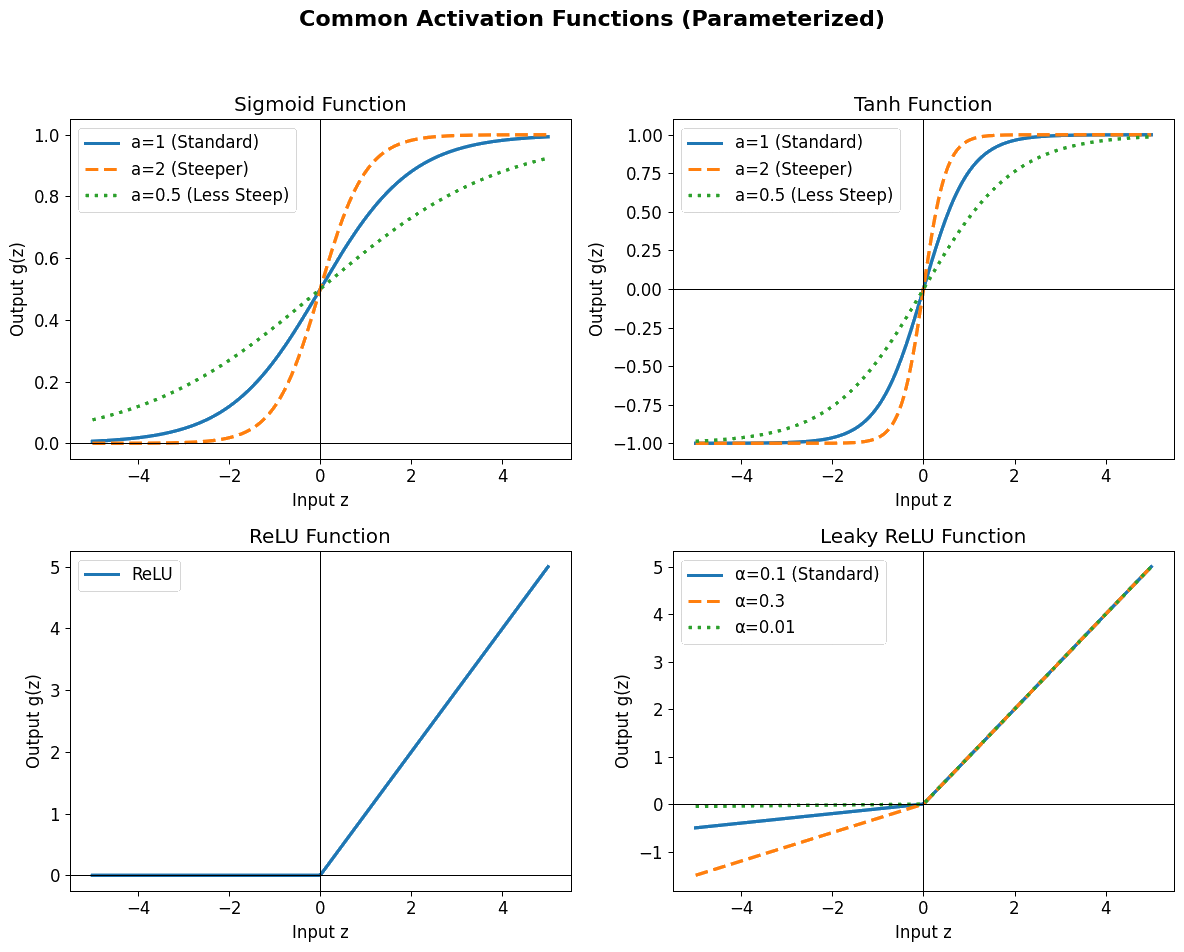
Sigmoid Squashes input to \((0, 1)\). Useful for binary classification output. Can suffer from vanishing gradients.

Tanh Squashes input to \((-1, 1)\). Zero-centered, often preferred over Sigmoid for hidden layers. Can also suffer from vanishing gradients.

ReLU (Rectified Linear Unit) Outputs input directly if positive, zero otherwise. Computationally efficient, helps mitigate vanishing gradients for positive inputs. Can suffer from 'dead neurons' if inputs are always negative.

LeakyReLU Similar to ReLU but allows a small gradient for negative inputs, preventing dead neurons.