We begin with a familiar problem: the one-dimensional Poisson equation on the unit interval \([0, 1]\) with homogeneous Dirichlet boundary conditions:

subject to boundary conditions:

This equation models diverse physical phenomena: heat conduction in a rod, deflection of a loaded beam, or electrostatic potential in one dimension. The function \(u(x)\) represents the unknown solution we seek, while \(f(x)\) is the prescribed source term.

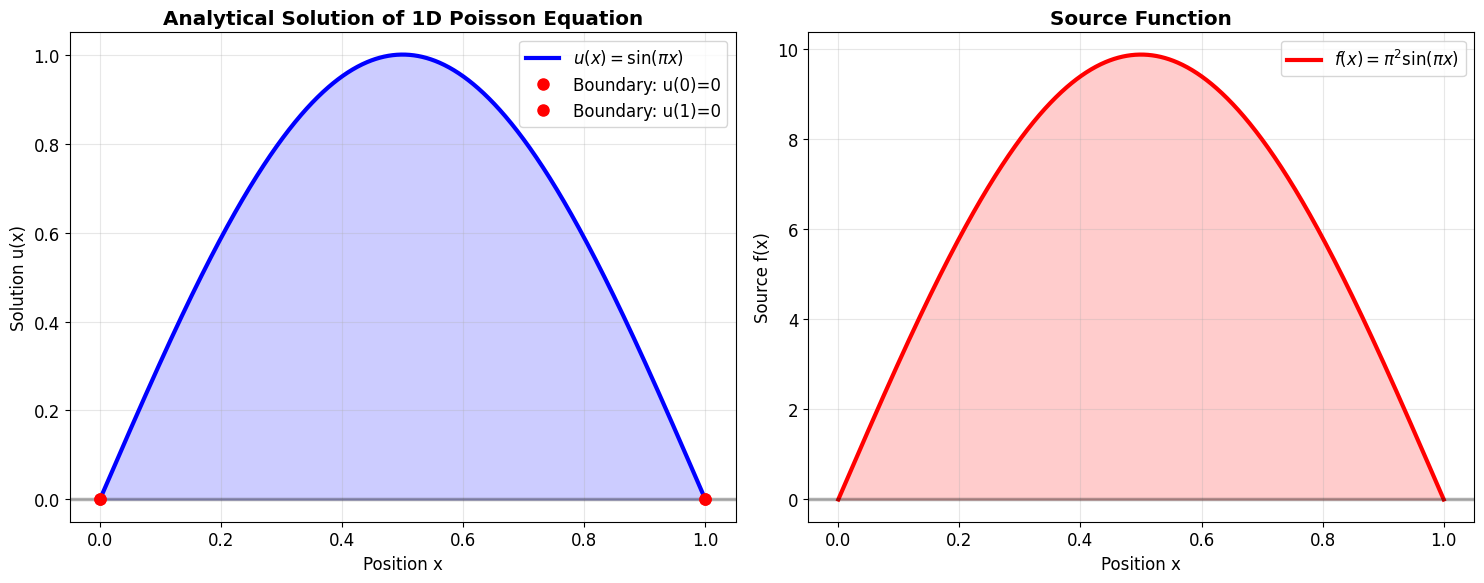
For our initial exploration, we choose a source term that gives a simple, known solution:

This choice yields the analytical solution:

We can verify this solution by direct substitution. The second derivative of \(u(x) = \sin(\pi x)\) is \(u''(x) = -\pi^2 \sin(\pi x)\), so:

The boundary conditions are satisfied: \(u(0) = \sin(0) = 0\) and \(u(1) = \sin(\pi) = 0 \checkmark\)