Forward mode AD computes derivatives by propagating derivative information forward through the computational graph, following the same path as the function evaluation.

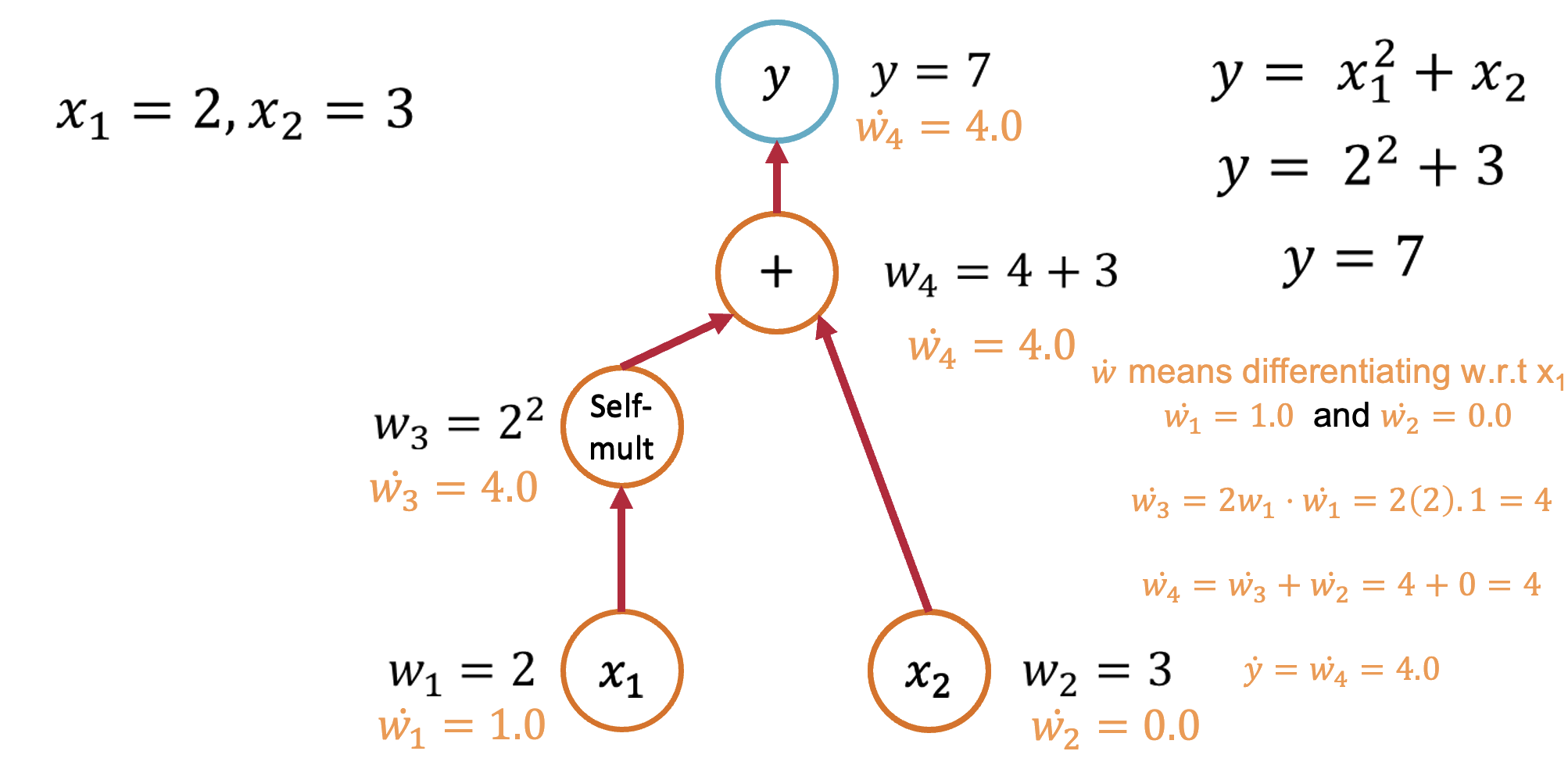
Forward Mode: Computing \(\frac{\partial y}{\partial x_1}\)

Starting with our function \(y = x_1^2 + x_2\), let's trace through the computation:

1. Seed the input: Set \(\dot{x}_1 = 1\) and \(\dot{x}_2 = 0\) (we're differentiating w.r.t. \(x_1\))
2. Forward propagation:
   • \(v_1 = x_1^2\), so \(\dot{v}_1 = 2x_1 \cdot \dot{x}_1 = 2x_1 \cdot 1 = 2x_1\)
   • \(y = v_1 + x_2\), so \(\dot{y} = \dot{v}_1 + \dot{x}_2 = 2x_1 + 0 = 2x_1\)
3. Result: \(\frac{\partial y}{\partial x_1} = 2x_1\)

Forward Mode: Computing \(\frac{\partial y}{\partial x_2}\)

To get the derivative w.r.t. \(x_2\), we seed differently:

1. Seed the input: Set \(\dot{x}_1 = 0\) and \(\dot{x}_2 = 1\)
2. Forward propagation:
   • \(v_1 = x_1^2\), so \(\dot{v}_1 = 2x_1 \cdot \dot{x}_1 = 2x_1 \cdot 0 = 0\)
   • \(y = v_1 + x_2\), so \(\dot{y} = \dot{v}_1 + \dot{x}_2 = 0 + 1 = 1\)
3. Result: \(\frac{\partial y}{\partial x_2} = 1\)