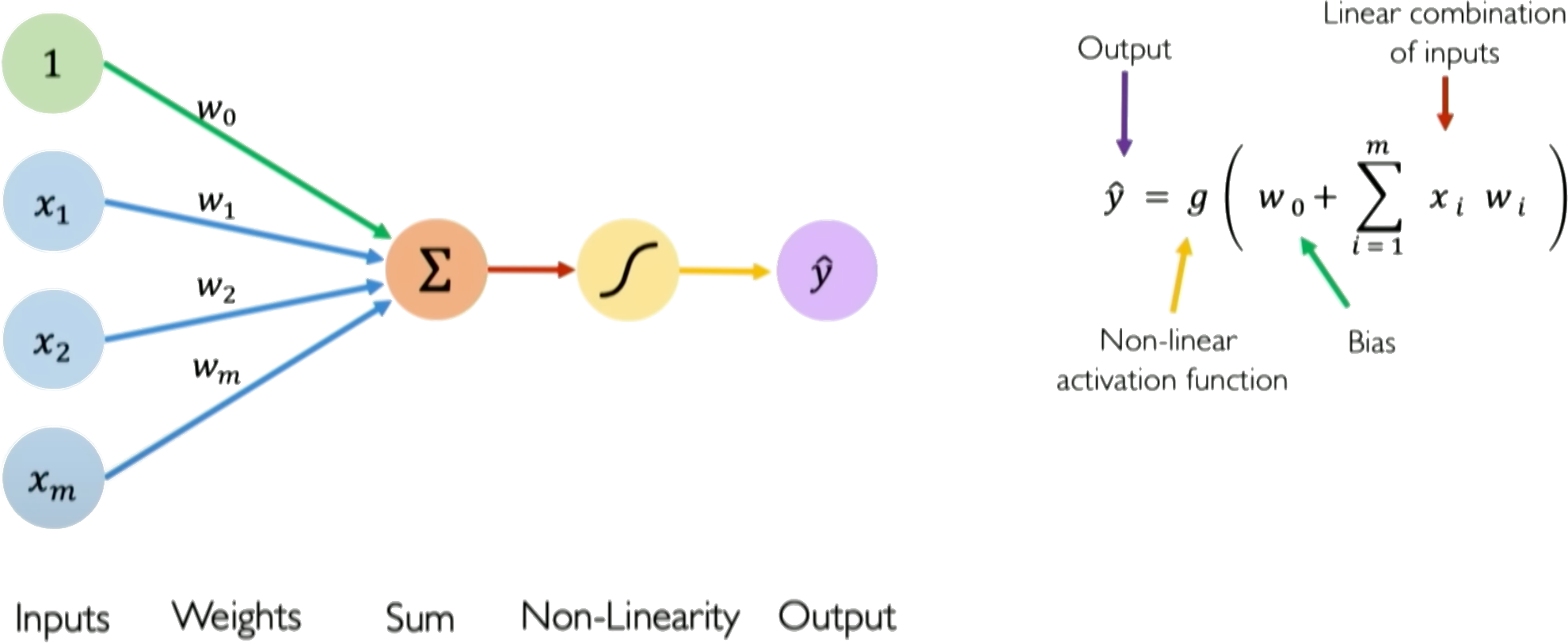
The fundamental unit of a neural network is the perceptron, or artificial neuron. It takes an input vector \(\boldsymbol{x}\), computes a weighted sum of its elements, adds a bias, and passes the result through an activation function \(g\).

Mathematically, for an input vector \(\boldsymbol{x} = [x_1, x_2, ..., x_n]\) and corresponding weights \(\boldsymbol{w} = [w_1, w_2, ..., w_n]\), with a bias \(b\), the operation is:

The output \(\hat{y}\) is then computed by passing it through an activation function:

Here, \(z\) is the pre-activation or 'logit' value, and \(g\) is the activation function. The activation function \(g\) introduces nonlinearity to allow the perceptron to learn complex mappings from inputs to outputs. Typical choices for \(g\) are sigmoid, tanh, or ReLU functions, though the original perceptron used a step function.

The perceptron can be trained via supervised learning, adjusting the weights and biases to minimize the loss between the predicted \(\hat{y}\) and the true label \(y^{\text{true}}\). Backpropagation combined with gradient descent can be used to iteratively update the weights to reduce the loss.

The key components of a perceptron are:

• Input vector \(\boldsymbol{x}\)
• Weight vector \(\boldsymbol{w}\)
• Weighted sum \(z = \boldsymbol{w}^T\boldsymbol{x}\)
• Nonlinear activation \(g\)
• Output prediction \(\hat{y}\)

The perceptron provides a basic model of a neuron, and multilayer perceptrons composed of many interconnected perceptrons can be used to build neural networks with substantial representational power. A perceptron takes a set of inputs, scales them by corresponding weights, sums them together with a bias, applies a non-linear step function, and produces an output. This simple model can represent linear decision boundaries and serves as a building block for more complex neural networks. In training, weights are updated based on the difference between the predicted output and the actual label, often using the Perceptron learning algorithm.

Resize Image