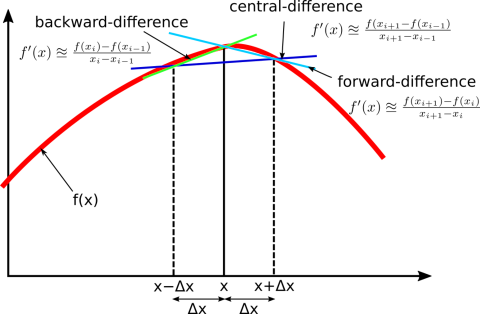
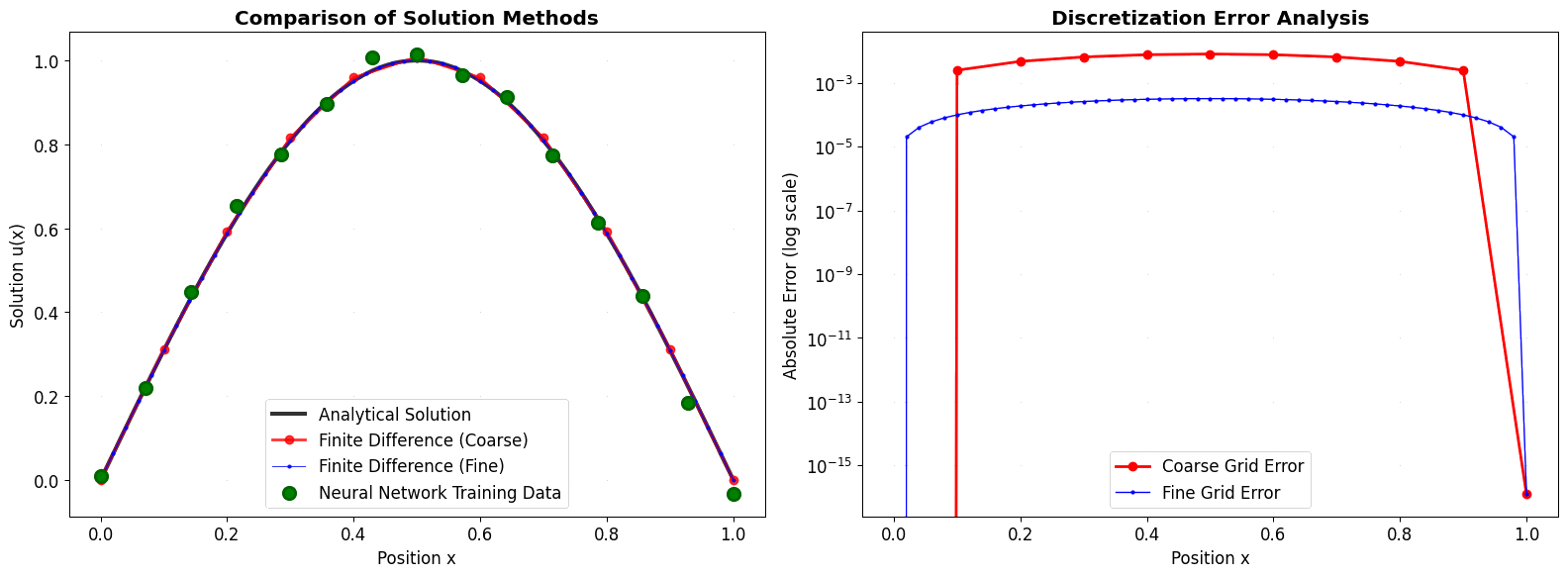
Traditional Methods: Finite Difference
Traditional numerical methods like the Finite Difference Method or Finite Element Method solve PDEs by discretizing the domain into a grid or mesh. They approximate the solution \(u(x)\) by finding its values at these specific, discrete points.
For example, the Finite Difference method approximates the second derivative:
\[\frac{d^2u}{dx^2} \approx \frac{u_{i+1} - 2u_i + u_{i-1}}{h^2}\]
This transforms the differential equation into a system of algebraic equations for the values \(u_i\) at grid points \(x_i\). The result is a discrete representation of the solution.
©
|
Cornell University
|
Center for Advanced Computing
|
Copyright Statement
|
Access Statement
CVW material development is supported by NSF OAC awards 1854828, 2321040, 2323116 (UT Austin) and 2005506 (Indiana University)
CVW material development is supported by NSF OAC awards 1854828, 2321040, 2323116 (UT Austin) and 2005506 (Indiana University)