Multi-Layer Perceptron
Physics-Informed Neural Networks (PINNs)
DeepONet: Operator Learning with Neural Networks
Differentiable Simulation
Graph Neural Network
Lab Setup

The Need for Depth - The XOR Problem: A Historical Turning Point

The XOR problem exposed fundamental limitations of true single-layer perceptrons, causing the 'AI winter' of the 1970s. This simple problem reveals why depth is essential.

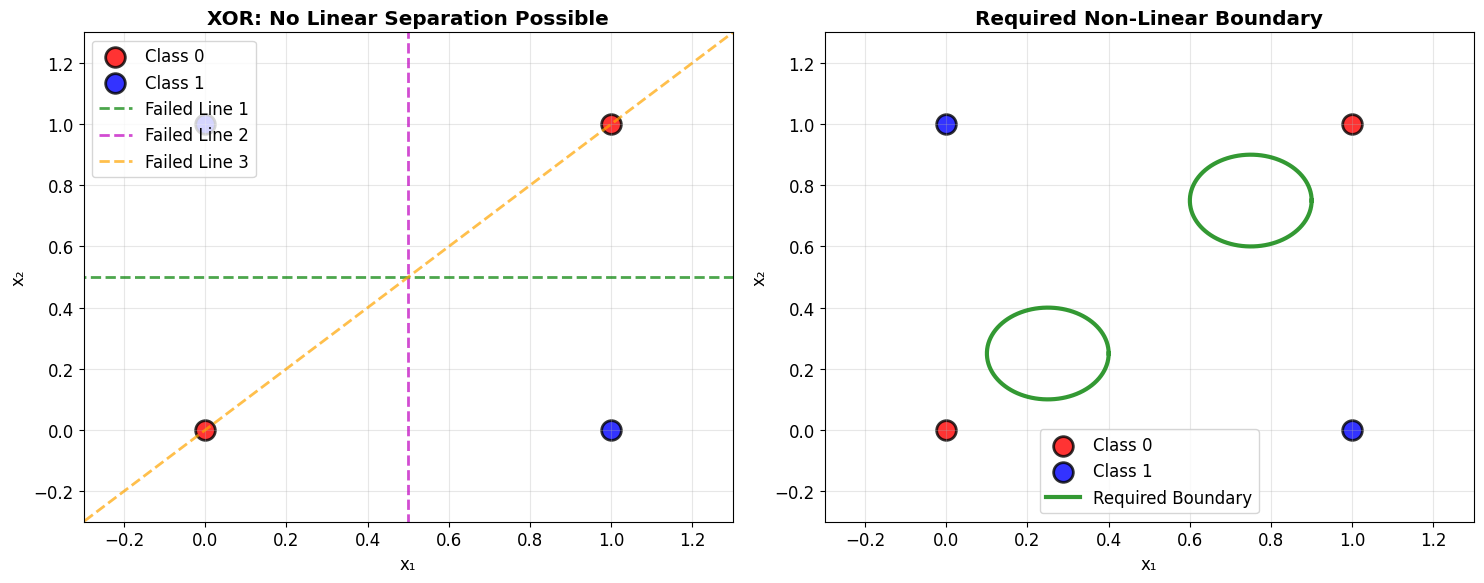
The crisis: No single line can separate these classes!

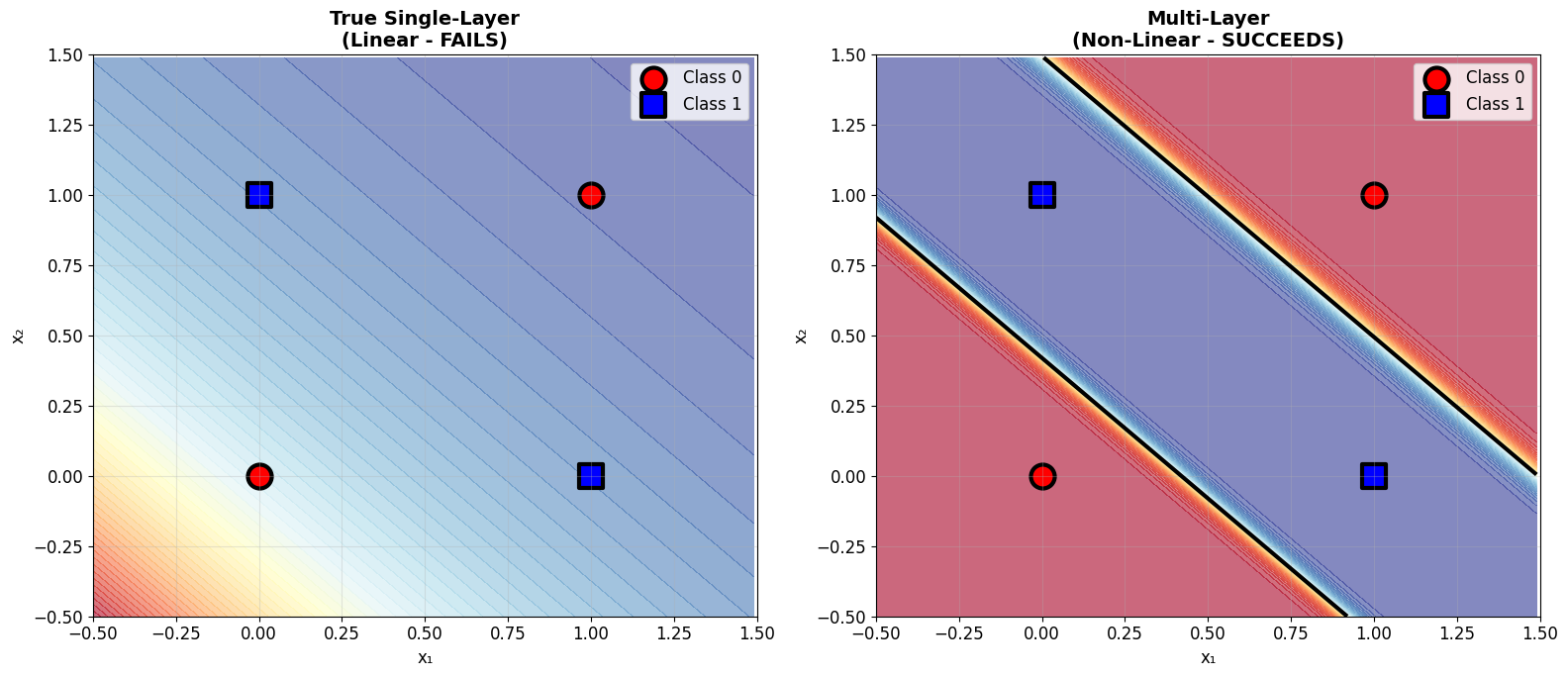
The Critical Distinction: True Single-Layer vs Multi-Layer

Historical confusion: What Minsky & Papert analyzed was a TRUE single-layer perceptron (Input → Output directly). This is different from our 'single-layer' networks that have hidden layers!

Architecture comparison:

  • True Single-Layer: Input → Output (NO hidden layers)
  • Multi-Layer: Input → Hidden → Output (1+ hidden layers)

The Historical Failure: True Single-Layer on XOR

Prediction: The true single-layer perceptron will fail spectacularly at XOR.

The Solution: Adding Hidden Layers

Hypothesis: Adding just ONE hidden layer should solve XOR completely.

Visualizing the Decision Boundaries
The Geometric Insight:

Linear vs non-linear decision boundaries.

Mathematical Explanation: Why Depth Solves XOR

True single-layer limitation:

\[ y = \sigma(w_1 x_1 + w_2 x_2 + b) \]

Decision boundary: \(w_1 x_1 + w_2 x_2 + b = 0\) (always a straight line)

Multi-layer solution: Decompose XOR into simpler operations

\[ h_1 = \sigma(w_{11} x_1 + w_{12} x_2 + b_1) \quad \text{(≈ OR gate)} \]
\[ h_2 = \sigma(w_{21} x_1 + w_{22} x_2 + b_2) \quad \text{(≈ AND gate)} \]
\[ y = \sigma(v_1 h_1 + v_2 h_2 + b_3) \quad \text{(≈ OR AND NOT)} \]

Result: XOR = (OR) AND (NOT AND) = compositional solution!

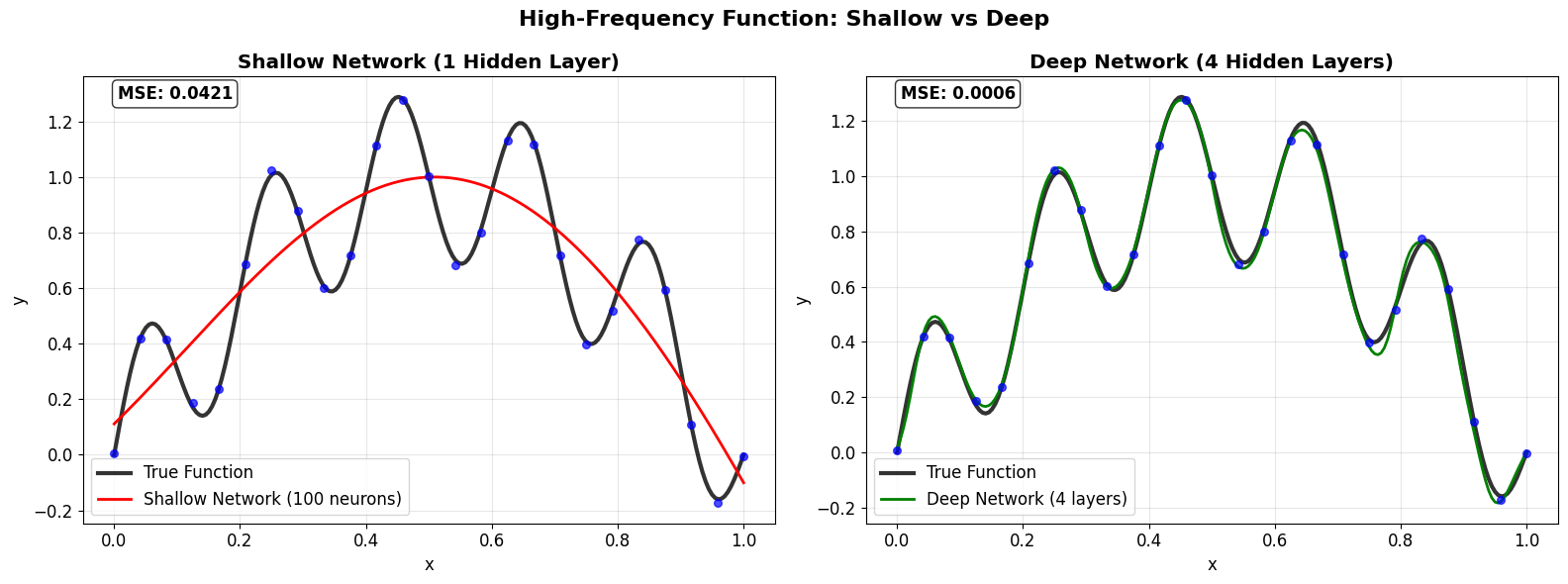
Beyond XOR: High-Frequency Functions

The deeper question: Does the depth advantage extend beyond simple classification?

Test case: High-frequency function \(f(x) = \sin(\pi x) + 0.3\sin(10\pi x)\)

Historical Timeline: From Crisis to Revolution

The XOR crisis and its resolution transformed AI:

Year Event Impact
1943 McCulloch-Pitts neuron Foundation laid
1957 Rosenblatt's Perceptron First learning success
1969 Minsky & Papert: XOR problem Showed true single-layer limits
1970s-80s 'AI Winter' Funding dried up
1986 Backpropagation algorithm Enabled multi-layer training
1989 Universal Approximation Theorem Theoretical foundation
2006+ Deep Learning Revolution Depth proves essential

The lesson: XOR taught us that depth is not luxury—it's necessity.

Why Depth Matters: The Four Key Insights

  1. Representation Efficiency
    • Shallow networks: May need exponentially many neurons
    • Deep networks: Hierarchical composition is exponentially more efficient
    • Example: XOR impossible with 1 layer, trivial with 2 layers
  2. Feature Hierarchy
    • Layer 1: Simple features (edges, basic patterns)
    • Layer 2: Feature combinations (corners, textures)
    • Layer 3+: Complex abstractions (objects, concepts)
    • Key insight: Real-world problems have hierarchical structure
  3. Geometric Transformation
    • Each layer performs coordinate transformation
    • Deep networks 'unfold' complex data manifolds
    • XOR example: Transform non-separable → separable
    • General principle: Depth enables progressive simplification
  4. Compositional Learning
    • Complex functions = composition of simple functions
    • Mathematical: \(f(x) = f_L(f_{L-1}(...f_1(x)))\)
    • Practical: Build complexity incrementally
    • Universal: Applies across domains (vision, language, science)

Back
 
Next
©  |   Cornell University    |   Center for Advanced Computing    |   Copyright Statement    |   Access Statement
CVW material development is supported by NSF OAC awards 1854828, 2321040, 2323116 (UT Austin) and 2005506 (Indiana University)