Now let's directly compare the performance of the soft and hard constraint methods.

Solution and Error Comparison

We plot both PINN solutions against the analytical solution and also visualize their absolute errors.

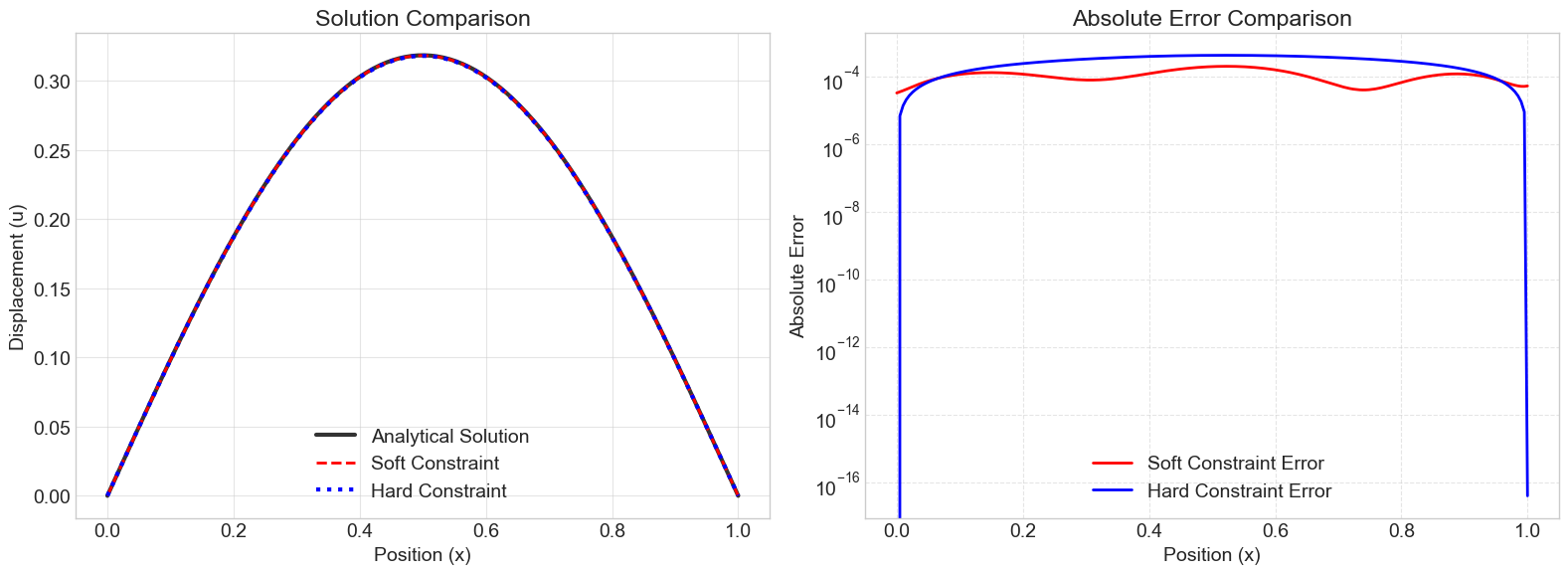
Discussion of Results

Both methods achieve a high degree of accuracy for this problem. The hard constraint method shows a slightly lower overall error (RMSE) and, by design, has zero error at the boundaries.

Trade-offs:

• Soft Constraints (Weak Enforcement):
  • Pros: Very flexible. The same approach can be used for different types of boundary conditions (Dirichlet, Neumann, Robin) without changing the network architecture. It's easy to implement.
  • Cons: Requires careful tuning of the loss weight (\( \lambda_{BC} \)). If the weight is too small, the BCs are not well-enforced. If it's too large, it can dominate the optimization and hinder convergence of the PDE part. Satisfaction of BCs is only approximate.
• Hard Constraints (Strong Enforcement):
  • Pros: Guarantees exact satisfaction of Dirichlet BCs. Simplifies the loss function, removing the need to balance competing PDE and BC loss terms, which can lead to more stable and faster training.
  • Cons: Less flexible. It requires designing a specific trial function \( \tilde{u}(x) \) for the exact geometry and boundary conditions of the problem. This can become very difficult or impossible for complex domains or more complicated BCs.

For problems with simple geometries and Dirichlet boundary conditions, the hard constraint method is often the superior choice due to its robustness and simplified training dynamics. For problems with complex geometries or other types of boundary conditions, the soft constraint method provides a more versatile and straightforward framework.