Multi-Layer Perceptron
Physics-Informed Neural Networks (PINNs)
DeepONet: Operator Learning with Neural Networks
Differentiable Simulation
Graph Neural Network
Lab Setup

Stage 1: Understanding the Forward Problem

Stage 1: Understanding the Forward Problem

Before tackling the inverse problem, let's understand the forward problem and generate our "experimental" data.

Analytical Solution

For our specific case with \( f(x) = -15x + 2 \) and homogeneous boundary conditions, the exact solution is:

\[ T(x) = \frac{15x^3 - 2x^2 - 13x}{6\kappa} \]
Key insight:

Notice how \( T(x) \) depends on \( \kappa \). Different values of \( \kappa \) give different temperature profiles!

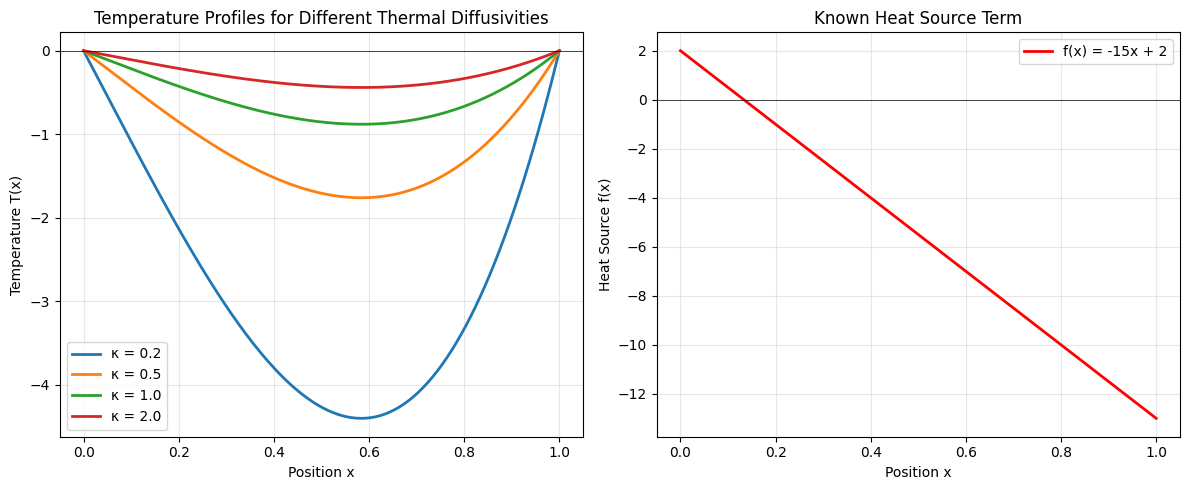
Creating "Experimental" Data

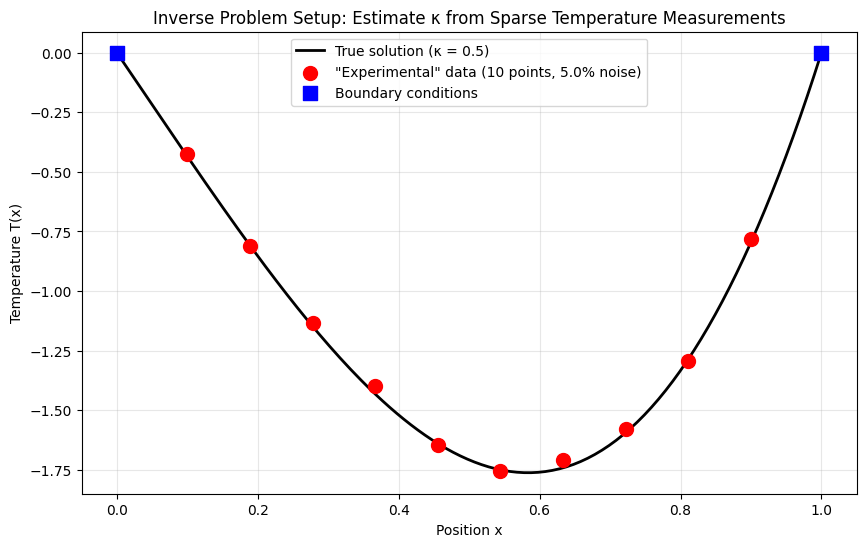
In a real experiment, we would measure temperature at a few locations. Let's simulate this with sparse, noisy measurements.

Back
 
Next
©  |   Cornell University    |   Center for Advanced Computing    |   Copyright Statement    |   Access Statement
CVW material development is supported by NSF OAC awards 1854828, 2321040, 2323116 (UT Austin) and 2005506 (Indiana University)