The PINN Architecture

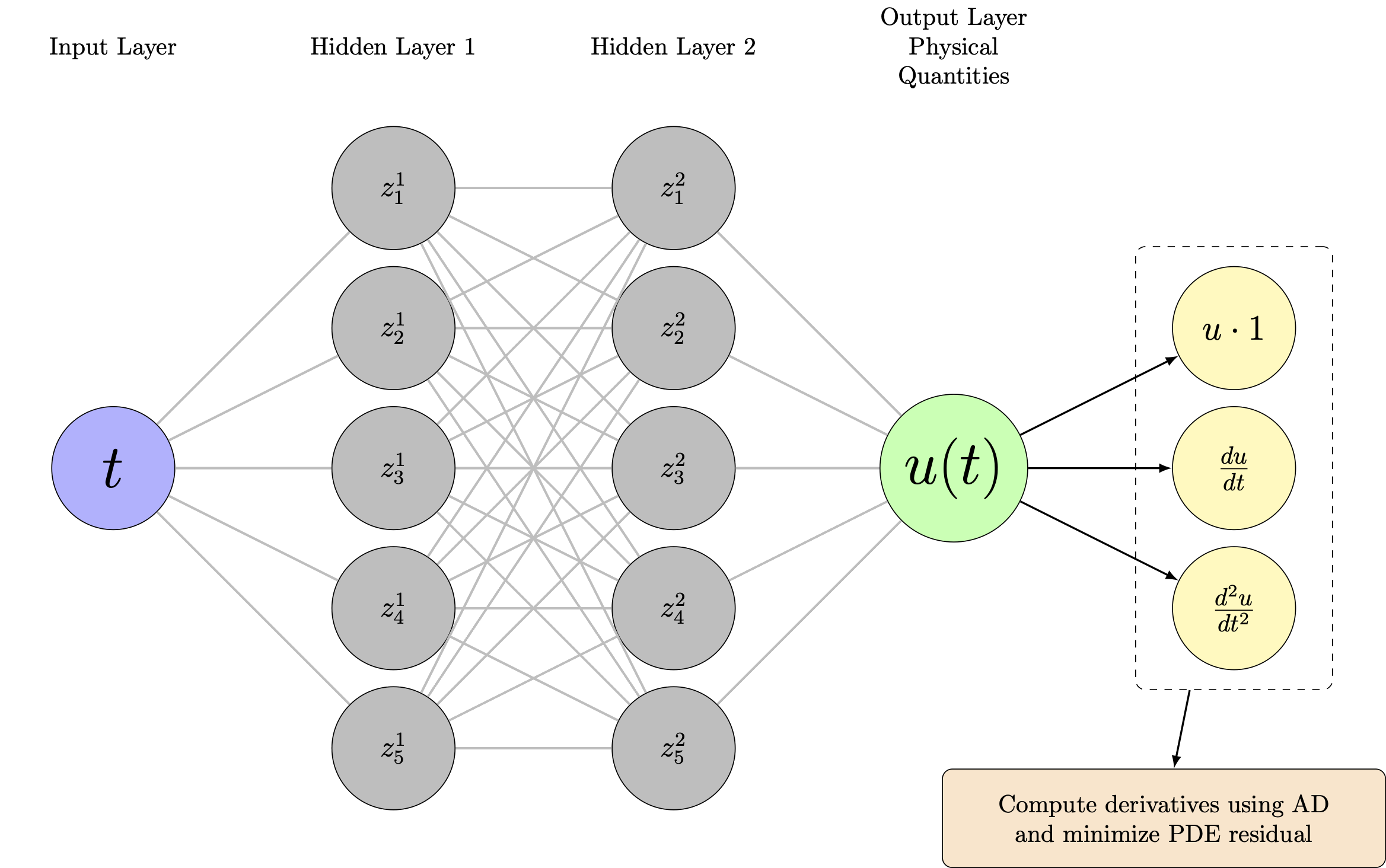
Same network, different loss function:

• Network still predicts \( \hat{u}_\theta(t) \)
• But now we compute derivatives via automatic differentiation
• Physics residual: \( \mathcal{R}_\theta(t) = m\frac{d^2\hat{u}_\theta}{dt^2} + c\frac{d\hat{u}_\theta}{dt} + k\hat{u}_\theta \)

The Physics Residual

Mathematical Foundation: If \( \hat{u}_\theta(t) \) is the exact solution, then:

PINN Strategy: Make this residual as small as possible everywhere in the domain.

Collocation Points: We evaluate the residual at many points \( \{t_j\} \) throughout \( [0,1] \), not just at data points.

The Complete PINN Loss Function

where:

Data Loss: \( \mathcal{L}_{\text{data}}(\theta) = \frac{1}{N_{\text{data}}} \sum_{i=1}^{N_{\text{data}}} |\hat{u}_\theta(t_i) - u_i|^2 \)

Physics Loss: \( \mathcal{L}_{\text{physics}}(\theta) = \frac{1}{N_{\text{colloc}}} \sum_{j=1}^{N_{\text{colloc}}} |\mathcal{R}_\theta(t_j)|^2 \)

Balance Parameter: \( \lambda \) controls data vs physics trade-off

Automatic Differentiation: The Secret Weapon

Critical Question: How do we compute \( \frac{d\hat{u}_\theta}{dt} \) and \( \frac{d^2\hat{u}_\theta}{dt^2} \)?

Answer: Automatic differentiation (AD) gives us exact derivatives!

• No finite differences
• No numerical errors
• Computed via chain rule through the computational graph
• Available in PyTorch, TensorFlow, JAX

Demonstration: Automatic Differentiation in Action

Let's see how automatic differentiation works in PyTorch: