Parameter Estimation in Heat Conduction

Learning Objectives:

• Understand the difference between forward and inverse problems
• Learn how PINNs solve inverse problems elegantly
• Master parameter estimation with sparse, noisy data
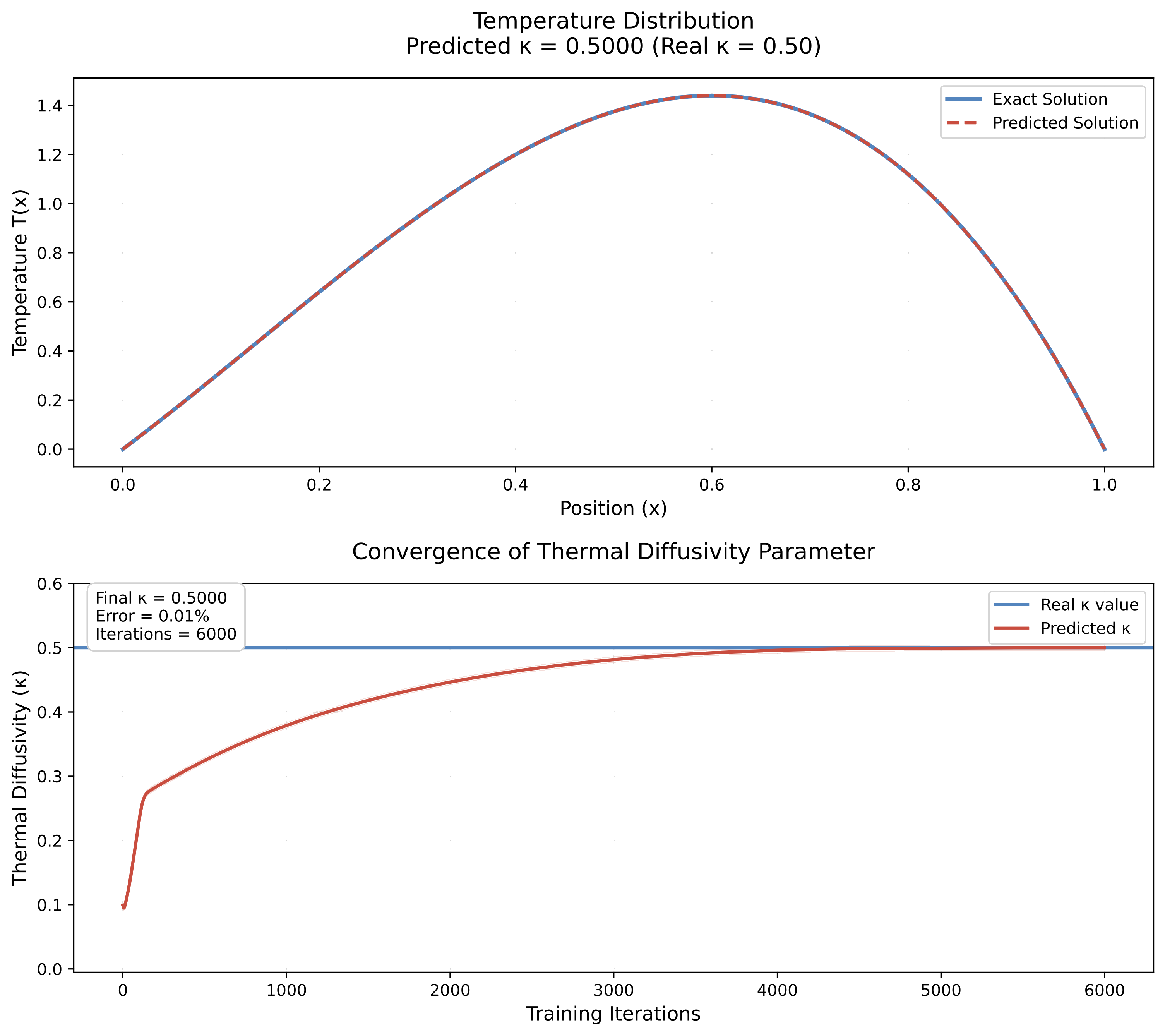
• Implement thermal diffusivity estimation from temperature measurements

Introduction: Forward vs Inverse Problems

The Forward Problem

In our previous PINN examples, we solved forward problems:

• Given: Complete physics (equations + parameters)
• Find: Solution function \( u(x,t) \)
• Example: Given spring constant \( k \) and damping \( c \), find oscillator motion \( u(t) \)

The Inverse Problem

In many real-world scenarios, we face inverse problems:

• Given: Some measurements of the solution \( u \)
• Find: Unknown physical parameters in the governing equations
• Example: From temperature measurements, determine thermal conductivity

Why Inverse Problems are Hard

Traditional Approach:

1. Guess parameter values
2. Solve forward problem (expensive numerical simulation)
3. Compare with measurements
4. Update guess and repeat

Problems:

• Computationally expensive (many forward solves)
• Sensitive to noise
• May not converge or find wrong parameters
• Requires good initial guesses

PINN Revolution: Solve forward and inverse problems simultaneously!