Stage 1: The Data-Only Approach (Why it Fails)
The Natural First Attempt: Train a neural network to fit the sparse data points.
Neural Network Architecture
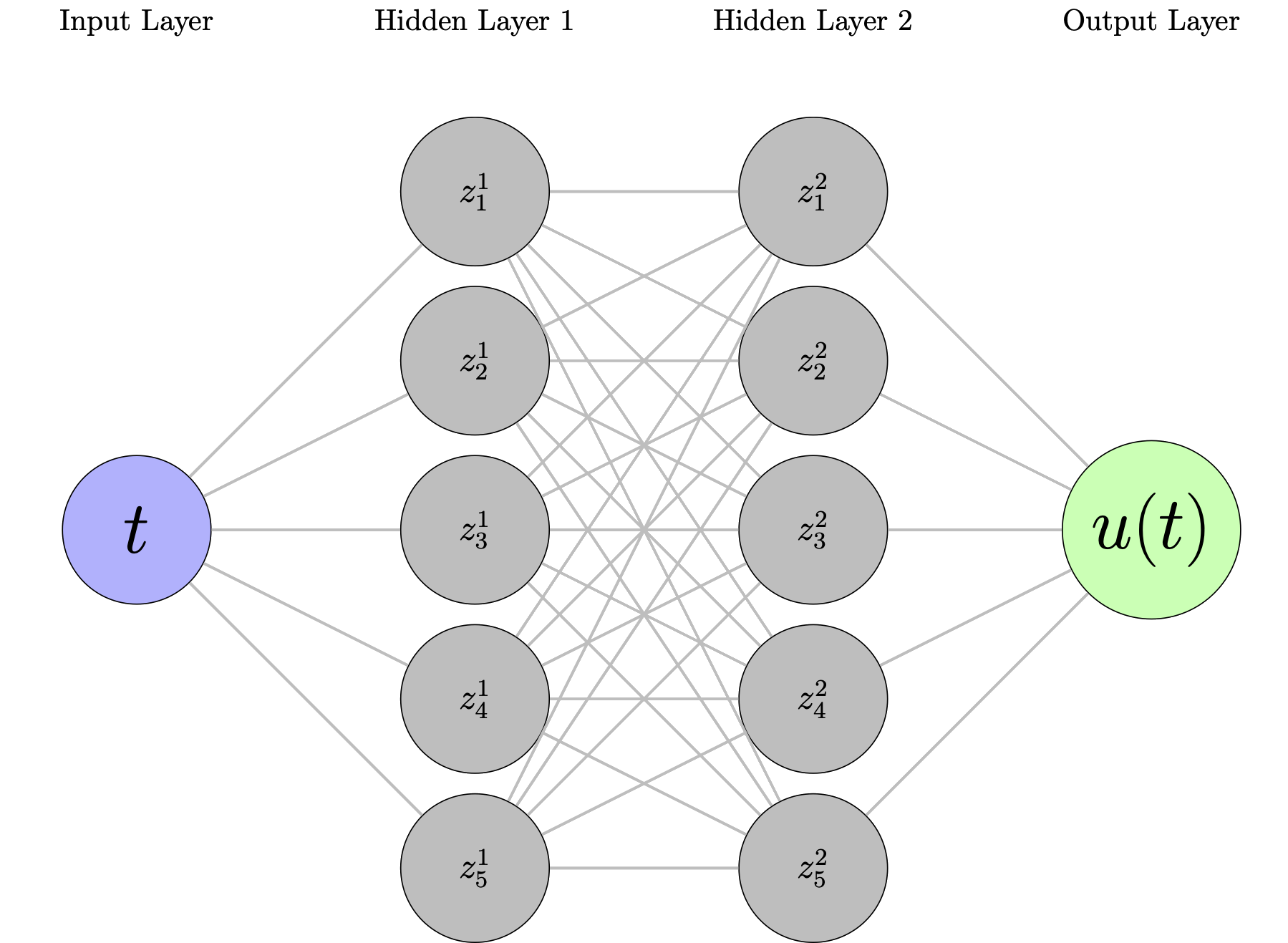
A simple feedforward network:
- Input: Time \( t \)
- Hidden layers: Dense layers with activation functions
- Output: Predicted displacement \( \hat{u}_\theta(t) \)
Loss function: Mean squared error between predictions and data
\[ \mathcal{L}_{\text{data}}(\theta) = \frac{1}{N} \sum_{i=1}^N |\hat{u}_\theta(t_i) - u_i|^2 \]
Training: Standard gradient descent to minimize \( \mathcal{L}_{\text{data}} \)
©
|
Cornell University
|
Center for Advanced Computing
|
Copyright Statement
|
Access Statement
CVW material development is supported by NSF OAC awards 1854828, 2321040, 2323116 (UT Austin) and 2005506 (Indiana University)
CVW material development is supported by NSF OAC awards 1854828, 2321040, 2323116 (UT Austin) and 2005506 (Indiana University)