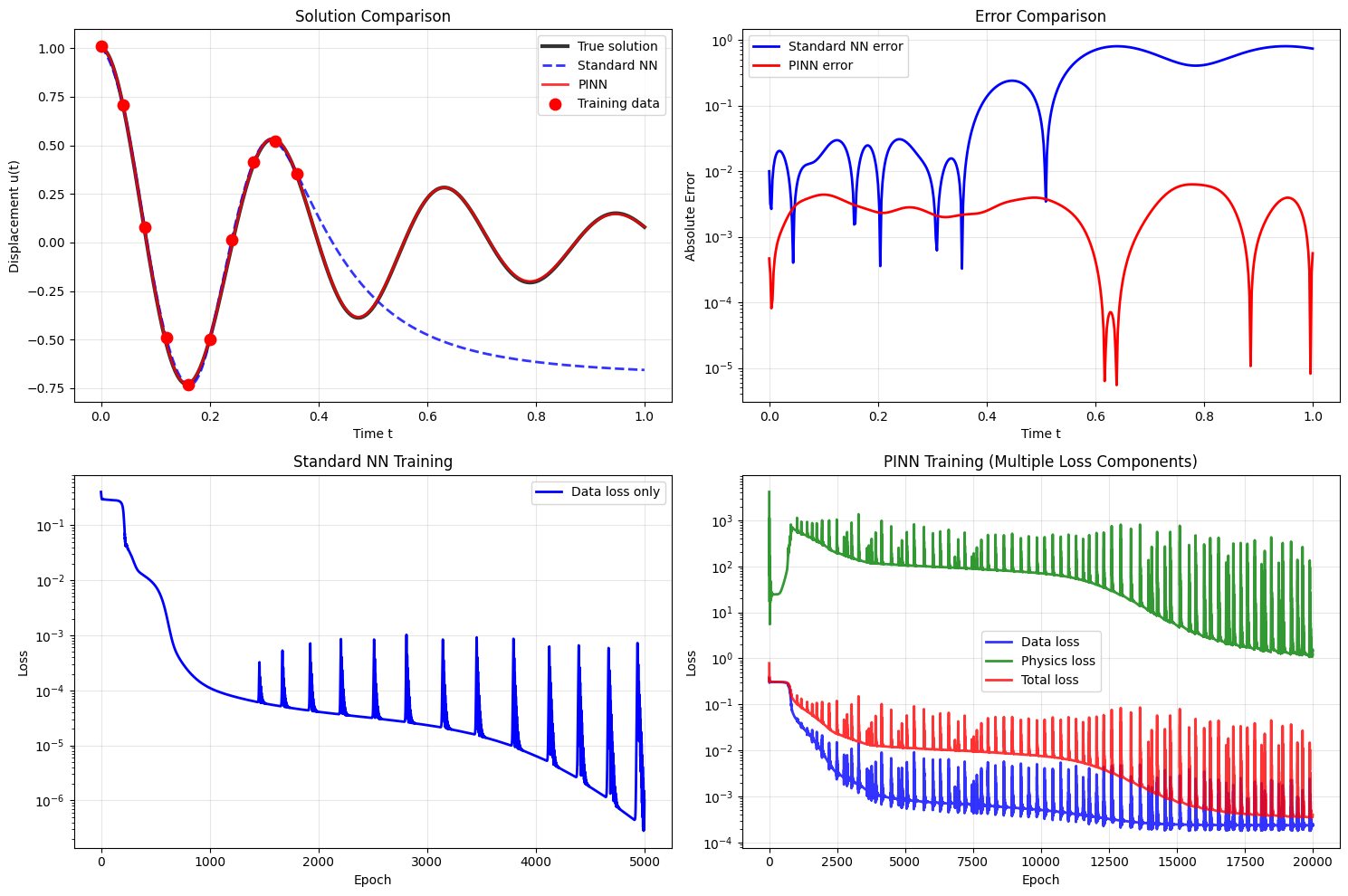
Direct Comparison: Standard NN vs PINN

What we expect to see:

• Standard NN: Fits data points but fails between them
• PINN: Fits data points AND follows physics everywhere

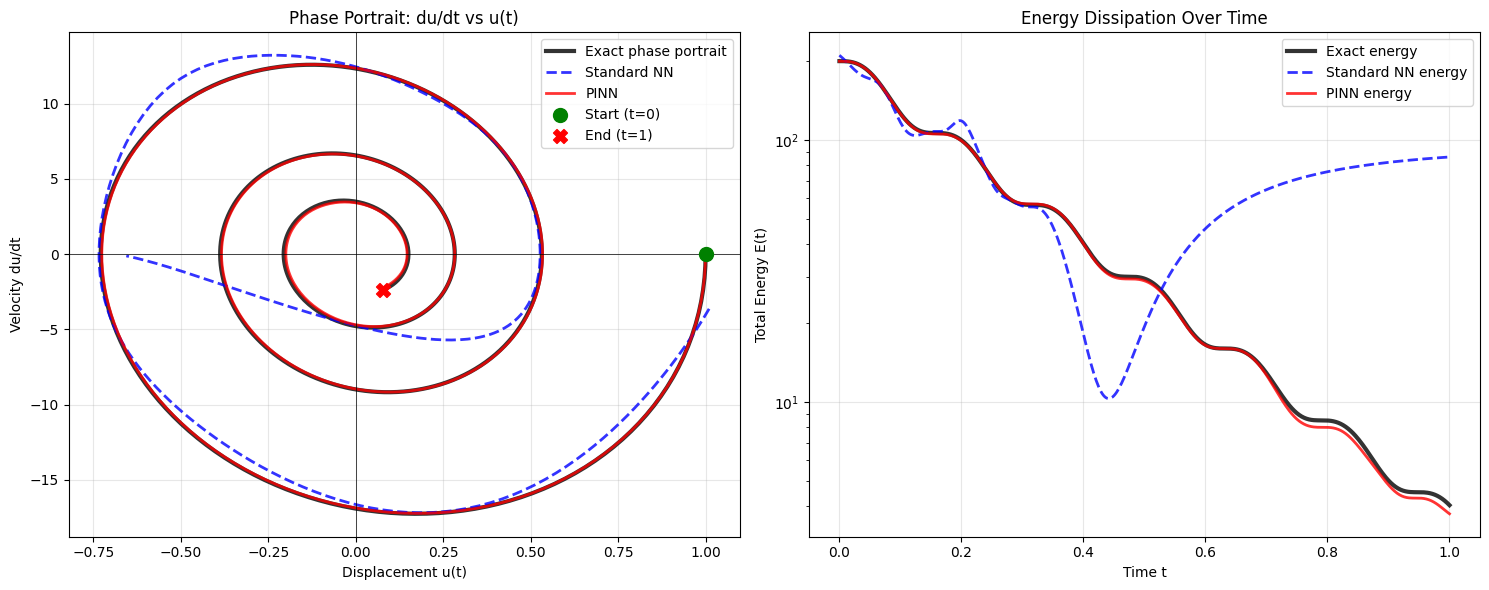
Phase Portrait Analysis: The Ultimate Physics Test

Critical Test: Can our neural networks capture this fundamental physical behavior?

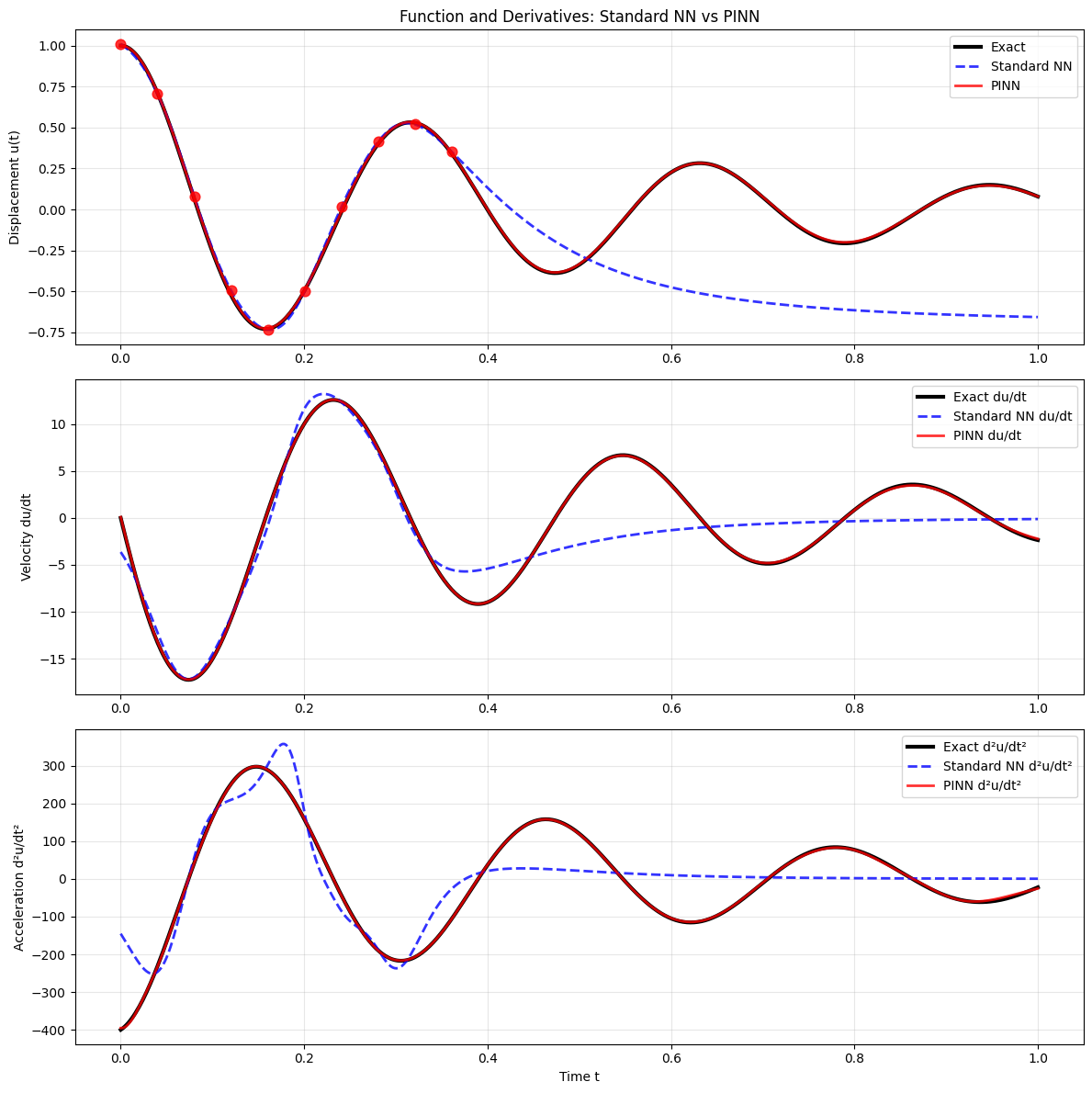
Deep Dive: Derivative Analysis

Critical Test: Can the PINN learn physically consistent derivatives?

Since we enforce the ODE through derivatives, the PINN should naturally learn correct \( \frac{du}{dt} \) and \( \frac{d^2u}{dt^2} \).